Get Ahead in Geometry: Solve Problems like a Pro with Over 1500 Illustrations and Drawings

Geometry: Open Problems

The ultimate goal may be to encourage mathematical thinking and problem-solving skills, and to foster a sense of community among those interested in geometry and mathematics more broadly.

Geometry Problems - Visual Index.
Online Education, School, College.

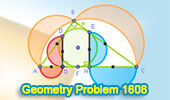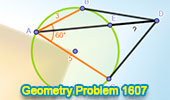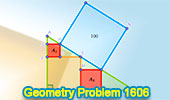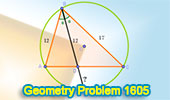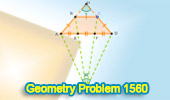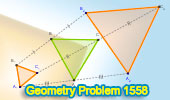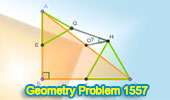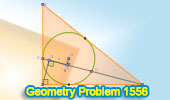Geometry Problem 1556: Right Triangle ABC and Inscribed Circle. The problem involves circle, chords, tangent, perpendicular lines, and congruence

Geometry Problem 1555: Find Length of DE. The problem involves chords, tangent, circles, and intersections of line

Geometry Problem 1554: Finding the Length of Side AB in Triangle ABC

Geometry Problem 1553: Solving for OC in Triangle ABC with Unique Angle Bisectors

Geometry Problem 1552: Exploring Angle C in Triangle ABC with Given Angle A and Side Lengths

Geometry Problem 1551: Unraveling Angle Relations in Cyclic Quadrilaterals: Solving for Angle GEJ: A High School Level Investigation

Geometry Problem 1550: Solving for Segment BD: An Angle Puzzle in Right Triangle ABC: A High School Level Investigation

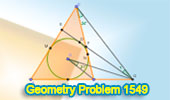Geometry Problem 1549: Unraveling the Geometric Mystery: Calculating Angle BGE with the Incircle and Tangent in Triangle ABC

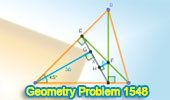Geometry Problem 1548: Exploring Segment DE Length in Triangle ABC with a 45-Degree Angle and Intersecting Altitudes

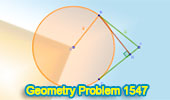Geometry Problem 1547: Tangents' Dance: Exploring B-to-AC Distance in a Circle's Grasp

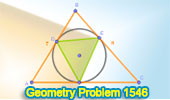Geometry Problem 1546: Discover the Hidden Geometry: Calculate Area of Contact Triangle DEF in Triangle ABC

Geometry Problem 1545: Unlock the Geometric Mystery: Calculate the Area of Triangle ABC with Inscribed Circle and Excenters!

Geometry Problem 1544: Challenge: Calculate the Area of a Triangle with Given Arc and Semicircle Intersections.

Geometry Problem 1543: Calculating the Area of Quadrilateral ABED in a Square with a Side Length of 20 and an Intersecting Arc.

Geometry Problem 1542: Unraveling a Geometric Puzzle with a Circumscribed Right Triangle and Square to the Same Circle for School and College.

Geometry Problem 1541 Challenge: Unveiling BG Length in an Inscribed Quadrilateral with Harmonic Quaternary Insight for Academic Pursuit.

Geometry Problem 1540: Solving for the Length of Chord in a Circle: Analyzing Intersections and Given Values for Academic Pursuits.

Geometry Problem 1539 Demystified: Unraveling the Lengths in an Isosceles Triangle with Altitude and Tangent Secrets!

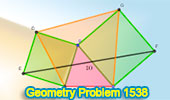Geometry Problem 1538: Unlocking the Secrets of Triangular Geometry: Solve for the Area of a Quadrilateral Using External Squares and a Segment Length.

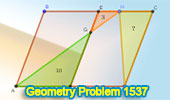Geometry Problem 1537 Challenge: Can You Solve for the Missing Area in a Parallelogram using Midpoints and Intersection Points?

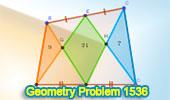Geometry Problem 1536: Discover the Power of Midpoints: Solving for Missing Areas in Quadrilaterals.

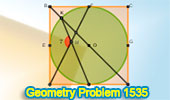Geometry Problem 1535: Crack the Code: Inscribed Circle in Square - Angle Challenge! Solve the Mystery.

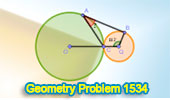Geometry Problem 1534: High School Brainteaser: Tangent Circles, Common External Tangent, and Angle Conundrums!.

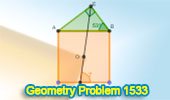Geometry Problem 1533: Discovering Relationships between Angles and Lines in an Exterior Right Triangle of a Square - A High School Challenge.

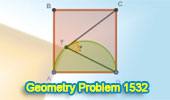Geometry Problem 1532: Crack the Code of Geometry Problem 1532: How to Find the Angle in a Square with a Tangent Semicircle! - A High School Challenge.

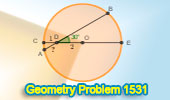Geometry Problem 1531: Discover How to Calculate the Length of a Chord in a Circle with Diameter Intersection and an Angle between the Diameter and Chord - A High School Challenge.

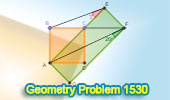Geometry Problem 1530: Unlock the Secrets of Geometric Angles: Calculate the Measurement of an Angle in a Square and Rectangle Figure Today! - A High School Challenge.

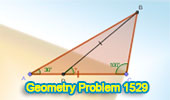Geometry Problem 1529: Unlock the Mystery of Triangles: Solving for the Missing Angle with 100-50-30 Degree Angles and Cevian Lengths - A High School Challenge.

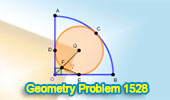Geometry Problem 1528: Cracking the Circle Code: Unveiling the Tangent and Angle of an Inscribed Circle within a 90-Degree Circular Sector.

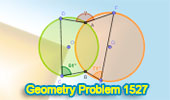Geometry Problem 1527: Discovering the Hidden Angle: Solving the Puzzle of Two Intersecting Circles.

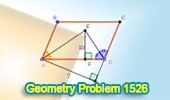Geometry Problem 1526: Mastering Geometry Problem-Solving: Discover the Distance Between Two Sides in a Parallelogram Using Bisectors and Distance Measures.

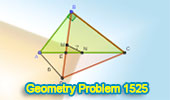Geometry Problem 1525 and a Thematic Poem.
Unveiling the Secrets of an Equilateral Triangle in Right Triangle Geometry: Finding the Midpoint Distance between Segments.

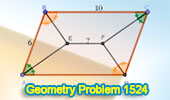Geometry Problem 1524 and a Thematic Poem.
Unlock the Mystery of Parallelograms: Discover the Length of Segment between the Intersecting Angle Bisectors.

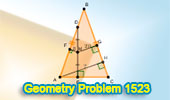Geometry Problem 1523 and a Thematic Poem.
Discover How to Calculate the Length of the Altitude in an Isosceles Triangle - Get Expert Geometry Tips Now!.

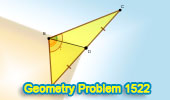Geometry Problem 1522 and a Thematic Poem.
Unlocking the Angle Measure of a Triangle with Median and Doubled Side Lengths.

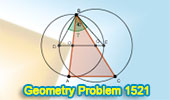Geometry Problem 1521 and a Thematic Poem.
Unlock the Secret to Finding the Measure of an Angle in a Triangle with Two Sides as Diameters of Circles.

Geometry Problem 1520 and a Thematic Poem.
Discovering Distances in a Rectangle with an Exterior Point: A Geometry Challenge.

Geometry Problem 1519 and a Thematic Poem.
Discover the Length of a Segment in a Parallelogram using Midpoints and Parallel Lines.

Geometry Problem 1518 and a Thematic Poem.
Boost Your Geometry Skills: Solve for the Number of Sides in an Equiangular Polygon with an Interior Point and Bisected Angle.

Geometry Problem 1517 and a Thematic Poem.
Unlocking Triangle Side Length: Solving with a Median and Two Angles. Difficulty Level: High School.

Geometry Problem 1516 and a Thematic Poem.
Finding the Length of a Side in an Equiangular Hexagon with Given Three Side Lengths. Difficulty Level: High School.

Geometry Problem 1515 and a Thematic Poem.
Mastering Triangle Distance Calculation: Find the Distance from the Intersection of Medians to an Exterior Line. Difficulty Level: High School.

Geometry Problem 1514 and a Thematic Poem.
Discover the Secret to Finding Distances in Regular Hexagons with Interior Squares. Difficulty Level: High School.

Geometry Problem 1513 and a Thematic Poem.
Solving the base in a Right Trapezoid with Double Angle and Sum of Two Sides. Difficulty Level: High School.

Geometry Problem 1512 and a Thematic Poem.
Finding the Length of a Segment in a Triangle with a Median and a Cevian with Given Ratio. Difficulty Level: High School.

Geometry Problem 1511 and a Thematic Poem.
Finding the Altitude of an Isosceles Triangle Using Distances from a Point on the Extension of the Base. Difficulty Level: High School.

Geometry Problem 1510 and a Thematic Poem.
Congruence of Triangles, Perimeter, Measurement. Difficulty Level: High School.

Geometry Problem 1509 and a Thematic Poem.
Congruence of Triangles in a Trapezoid and a Square, Measurement. Difficulty Level: High School.

Geometry Problem 1508.
Understanding Triangle Geometry: Isosceles, Equilateral, Quadrilateral, Angular. Difficulty Level: High School.

Geometry Problem 1507.
Understanding Triangle Geometry: Double Angles, Altitudes, and Measurements. Difficulty Level: High School.

Geometry Problem 1506.
Parallel Rays, Angles, Corresponding, Alternate. Difficulty Level: High School.

Geometry Problem 1505.
Parallel Rays, Angles, and Bisector, Corresponding, Alternate, Conjugate. Difficulty Level: High School.

Geometry Problem 1504 and Poem.
Squares, Equilateral Triangle, Parallel, Angle. Difficulty Level: High School.

Geometry Problem 1503.
Triangle, Incircle, Tangent, Congruence, Perpendicular.

Geometry Problem 1502.
Right Triangle, Incircle, Inradius, Geometric Mean of 2 Inradii, Angle Bisector, Perpendicular, Tangential Quadrilateral.

Geometry Problem 1501.
Square, Exterior Point, Congruent Angles, Segment, Measurement.

Geometry Problem 1500.
Circle, Perpendicular, Tangent, Secant, Cyclic Quadrilateral, Parallel, Similarity, Measurement.

Geometry Problem 1499.
Triangle, Angles, Cevian, Congruence, Isosceles, Equilateral, Auxiliary Construction.

Geometry Problem 1498.
Intersecting Circles, Diameter, Common Chord, Secant, Cyclic Quadrilateral, Concurrent Lines, Concyclic and Collinear Points.

Geometry Problem 1497.
Triangle, Transversal, Same Ratio, Proportionality, Isosceles, Double Angle.

Geometry Problem 1496.
Triangle, Congruence, Isosceles, Double Angle, 30 Degrees.

Geometry Problem 1495.
Circle, Parallel Chords, 30 Degree Angle, Radius Squared.

Geometry Problem 1494.
Parallelogram, Midpoints, Octagon, Areas.

Geometry Problem 1493.
Four Squares, Parallelogram, Auxiliary Lines.

Geometry Problem 1492.
Right Triangle, Altitude, Incenters, Angle, Measurement.

Geometry Problem 1491.
Cyclic Quadrilateral, Diagonal, Incircle, Angle, Measurement.

Go to page: Previous | 1 | 10 | 20 | 30 | 40 | Next