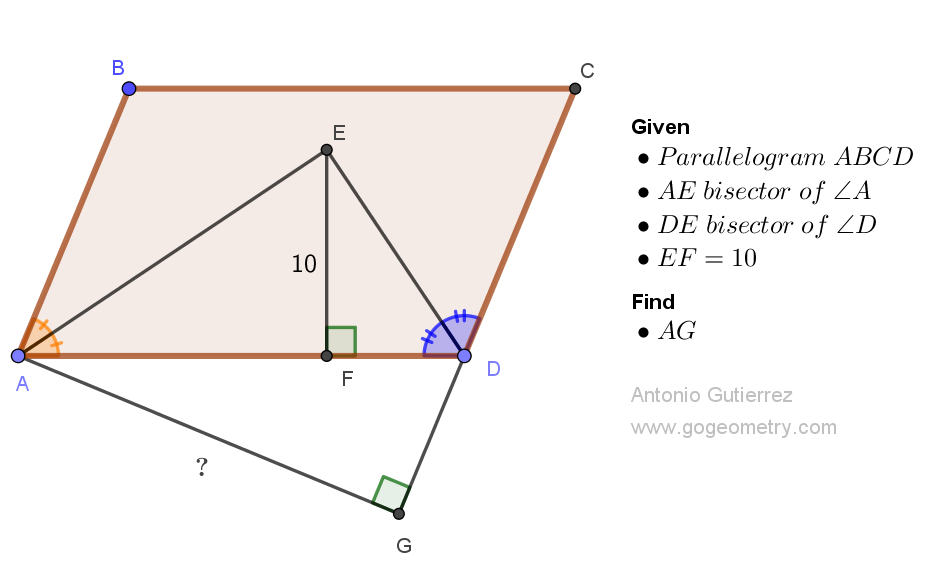
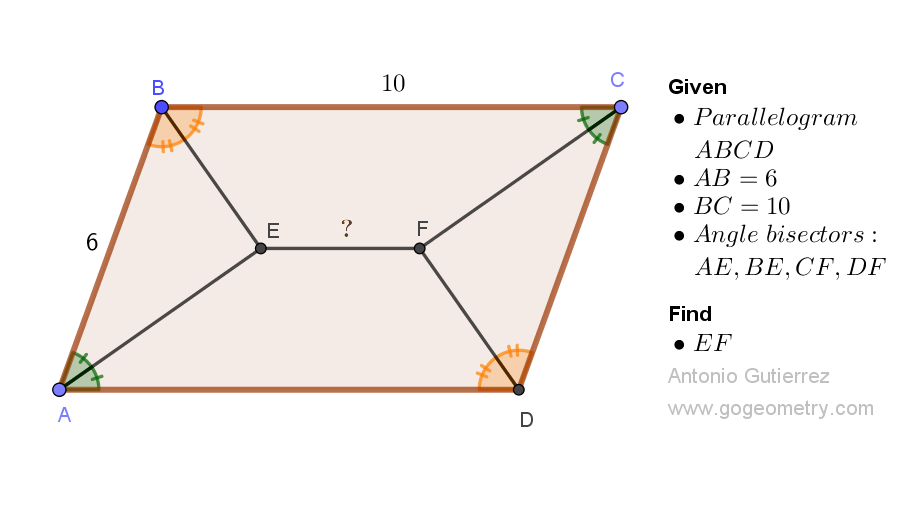
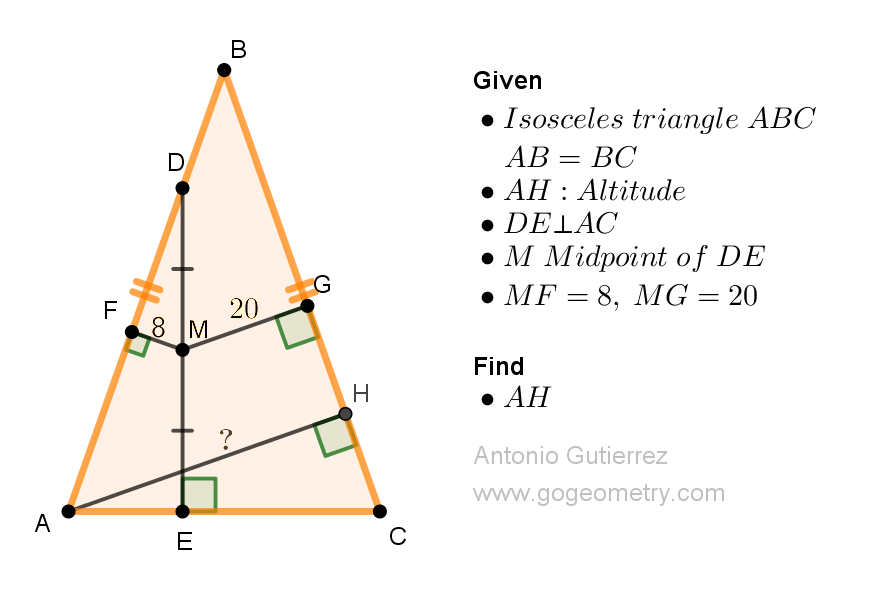
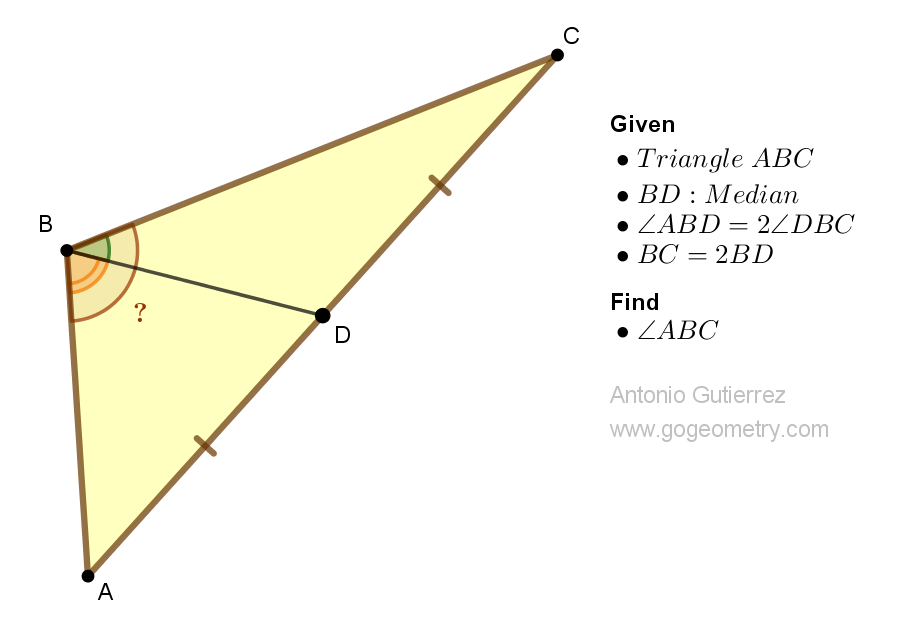
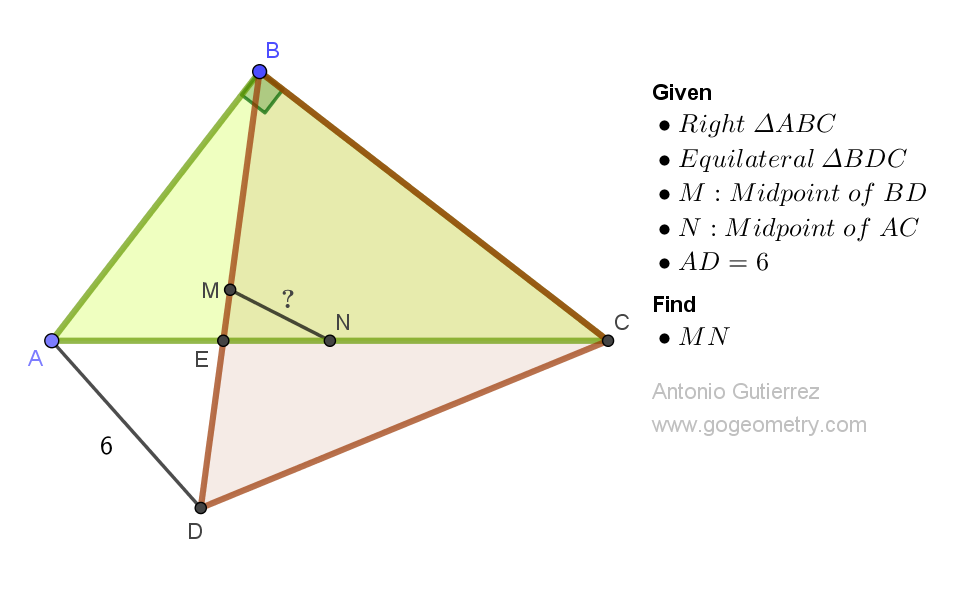
Geometry Problem 1525: Unveiling the Secrets of an Equilateral Triangle in Right Triangle Geometry: Finding the Midpoint Distance between Segments. Difficulty Level: High School.

Consider a right triangle ABC. Let BE be a cevian, or a line segment that connects vertex B to a point on side AC. Extend the cevian BE to a point D such that triangle BDC is equilateral. If the length of segment AD is 6 units, find the distance between the midpoints of segments BD and AC.

Geometry Problem 1525: Unveiling the Secrets of Equilateral Triangles in Right Triangle Geometry: Finding the Midpoint Distance between Segments

View or post a solution

Geometry Tips Now!

Concept Definition Theorem / Comment
Triangle A polygon with three sides and three angles. The sum of the angles in a triangle is 180 degrees.
Isosceles triangle An isosceles triangle is a triangle that has two sides of equal length. In an isosceles triangle, the altitudes relative to congruent sides are congruent.
Right triangle A right triangle is a type of triangle that has one of its interior angles measuring exactly 90 degrees (a right angle). The side opposite to the right angle is called the hypotenuse, while the other two sides are called the legs. In a right triangle, the length of the median to the hypotenuse is equal to half the length of the hypotenuse.
Equilateral Triangle An equilateral triangle is a type of triangle in which all three sides have the same length. Equilateral triangles are also known as regular triangles, since they have a high degree of symmetry and uniformity. In an equilateral triangle, all three angles have the same measure and are each 60 degrees.
Midpoint The point that divides a line segment into two equal parts. The midpoint theorem for triangles, also known as the mid-segment theorem, states that the segment connecting the midpoints of two sides of a triangle is parallel to the third side and half of its length.
Parallel lines Two lines in a plane that do not intersect. If two parallel lines are cut by a transversal, then the alternate interior angles are congruent, the corresponding angles are congruent, and the consecutive interior angles are supplementary.
Congruence Two triangles are said to be congruent if all corresponding sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.. There are several ways to prove that two triangles are congruent, including the Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Hypotenuse-Leg (HL) criteria.
Auxiliary line Auxiliary line is a line that is added to a diagram in order to help prove a theorem or solve a problem. Often, an auxiliary line is drawn to create additional congruent or similar triangles, to create parallel lines, or to create right angles. The use of auxiliary lines can simplify a problem or make a proof more straightforward. However, it is important to ensure that the auxiliary line does not create any new intersections or angles that were not present in the original diagram.
 

Discover Even More: See Also...

Problem 1526

Geometry Problem 1526: Mastering Geometry Problem-Solving: Discover the Distance Between Two Sides in a Parallelogram Using Bisectors and Distance Measures

Problem 1524

Geometry Problem 1524: Unlock the Mystery of Parallelograms: Discover the Length of Segment between the Intersecting Angle Bisectors

Problem 1523

Geometry Problem 1523: Discover How to Calculate the Length of the Altitude in an Isosceles Triangle - Get Expert Geometry Tips Now!

Problem 1522

Geometry Problem 1521: UUnlocking the Angle Measure of a Triangle with Median and Doubled Side Lengths. Difficulty Level: High School.

Problem 1521

Geometry Problem 1521: Unlock the Secret to Finding the Measure of an Angle in a Triangle with Two Sides as Diameters of Circles. Difficulty Level: High School.

 

Thematic Poem:
Unveiling the Secrets of Equilateral Triangles: A Geometric Odyssey

Behold, a problem of geometry
Of equilateral triangles and right angles, you see
A mystery to unravel, a secret to unveil
To find the midpoint distance, without fail

With ruler in hand and pencil in sight
We embark on a quest to shed some light
On the world of triangles, where numbers reign
And the beauty of shapes, we shall attain

Through angles acute and angles obtuse
We calculate and measure, with no excuse
For the midpoint distance, we must find
And unravel the secrets of the equilateral kind

Oh, the joys of math, how it puzzles the mind
Yet, with perseverance, we shall unwind
The mysteries of triangles, and in the end
We'll be triumphant, with knowledge to transcend

So let us embrace this geometry problem
With courage and tenacity, we shall solve them
And in the world of math, we shall prevail
Unveiling the secrets of equilateral triangles, without fail.

If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.

Recent Additions

Geometry Problems
Open Problems
Visual Index
All Problems
Triangle
Isosceles Triangle
Equilateral Triangle
Right Triangle
Midpoint
Perpendicular lines
Parallel lines
Congruence
View or Post a solution 

Search our site with Google: