Geometry Problem 1575: Proving an Angle Bisector in a Triangle Involving an Altitude, Midpoint, and Excircle. A High School and College Challenge

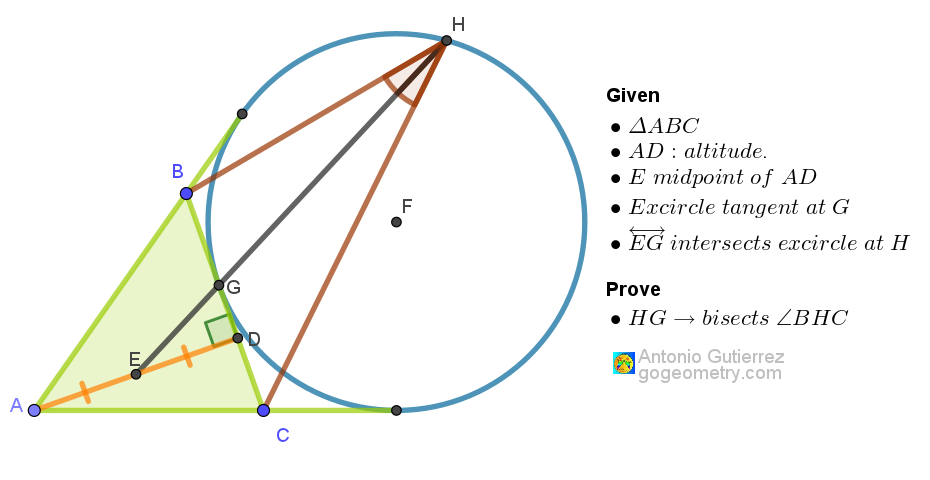
In triangle ABC, let E be the midpoint of altitude AD from A to BC. The excircle opposite C is tangent to BC at G, and line EG intersects the excircle at H. Prove that HG bisects angle BHC.

Uncover and share solutions to this problem.

Key Definitions and Descriptions

Key Term	Description
Triangle	The geometric figure ABC, consisting of three sides and three angles.
Altitude	The perpendicular segment AD from vertex A to side BC in triangle ABC.
Midpoint	The point E that divides the altitude AD into two equal segments.
Excircle	The circle opposite vertex C that is tangent to side BC of triangle ABC at point G.
Tangency Point	Point G where the excircle opposite C is tangent to BC.
Perpendicular	The line segment AD, which is perpendicular to side BC of triangle ABC.
Intersection	The point H where line EG intersects the excircle opposite C.
Angle Bisector	The line HG that bisects angle BHC in the geometric problem.
Bisects Angle	To divide an angle into two equal parts. In this problem, line HG bisects angle BHC.

---

Flyer of problem 1575 using iPad Apps