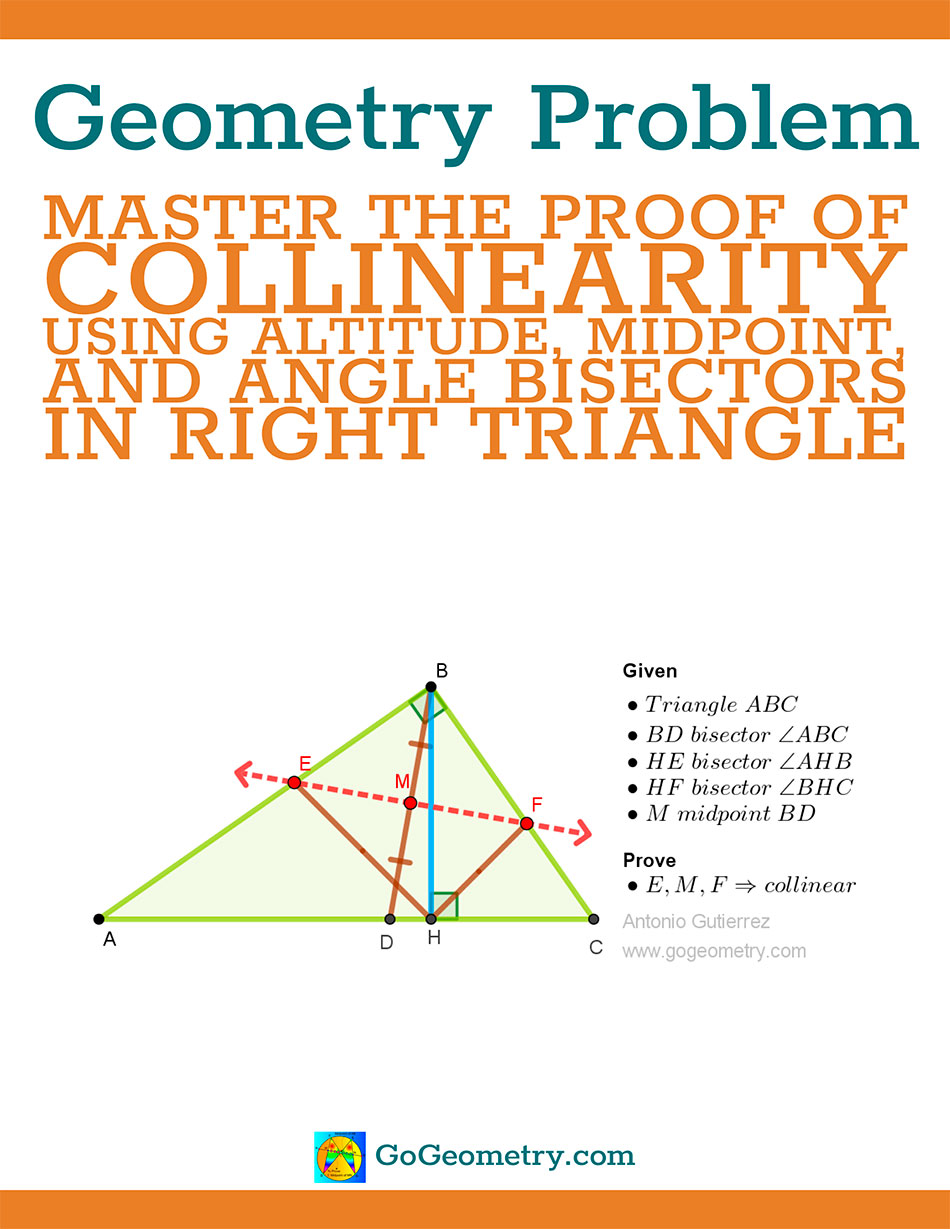
Geometry Problem 1562: Proof of Collinearity in a Right-angled Triangle involving the Altitude, Angle bisectors, and Midpoint.

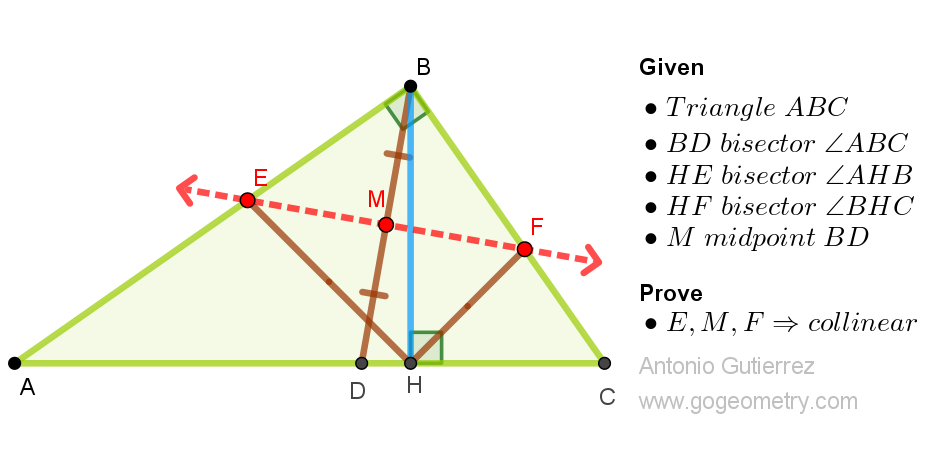
In a right-angled triangle ABC, where angle ABC is 90 degrees, let BH be the altitude from B to AC and BD be the bisector of angle ABC. The bisector of angle AHB intersects AB at E, and the bisector of angle BHC intersects BC at F. If M is the midpoint of BD, prove that the points E, M, and F are collinear.

Diagram of right-angled triangle ABC with altitude, bisectors, and midpoint proving collinearity. Geometry Problem 1562.

Right triangle stands tall,
Bisectors meet, paths align,
E, M, F in line.

Academic Levels: Suitable for High School and College Mathematics Education

Uncover and share solutions to this problem.

Key Definitions and Descriptions

Key	Description
Right-Angled Triangle ABC	A triangle with one angle measuring 90 degrees, with vertices labeled as A, B, and C.
Angle ABC	The right angle (90 degrees) in the triangle, located at vertex B.
Altitude BH	A perpendicular line segment from vertex B to the hypotenuse AC.
Bisector BD	A line segment from vertex B that bisects angle ABC, meeting AC at point D.
Point E	The point where the bisector of angle AHB intersects side AB.
Point F	The point where the bisector of angle BHC intersects side BC.
Midpoint M	The point that is exactly halfway along BD.
Collinear Points E, M, F	The points E, M, and F lie on a single straight line.