Geometry Problem 1567: Finding Tangent Distances in a Circumscribed Isosceles Trapezoid. Academic Levels: Suitable for High School and College Mathematics Education
Given a circumscribed isosceles trapezoid ABCD about a circle with bases BC = 8 and AD = 12 units, determine the length of the segment joining the points of tangency on sides AB and CD.
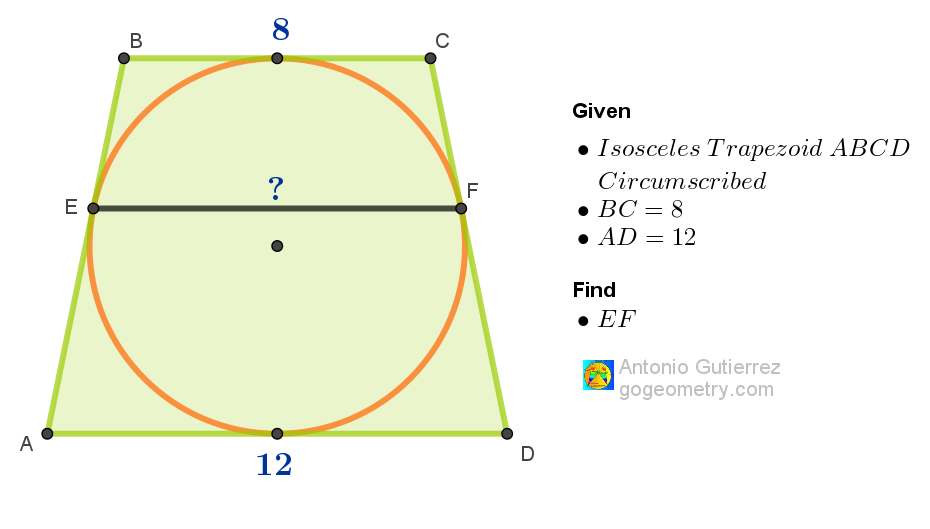
A circle within,
Tangents touch trapezoid's sides,
Solve the distance now.
Uncover and share solutions to this problem.
Key Definitions and Descriptions
| Vocabulary | Description |
|---|---|
| Isosceles Trapezoid | A trapezoid with a pair of opposite sides that are equal in length. |
| Circumscribed | A figure that is drawn around another, touching it at points but not cutting it. |
| Tangential trapezoid, also called a Circumscribed Trapezoid | A trapezoid whose four sides are all tangent to a circle within the trapezoid |
| Circle | A round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the center). |
| Bases (BC and AD) | The two parallel sides of the trapezoid. Here, BC = 8 units and AD = 12 units. |
| Points of Tangency | The points where a circle touches a line or another circle. |
| Segment Joining Points of Tangency | The length of the segment connecting the points where the circle touches sides AB and CD of the trapezoid. |
Flyer of problem 1567 using iPad Apps

Read more, explore further
Geometry Problems
Open Problems
Visual Index
All Problems
Trapezoid
Triangle
Quadrilateral
Tangential or Circumscribed Quadrilateral
Circle
Chord
Circle Tangent Line
Similarity
View or Post a solution
Search our site with Google: