Geometry Problem 1580: 60-Degree Triangle Challenge: Find AD with Excenter and Circumcircle Clues! Perfect for High School and College Students!
In triangle ABC, angle B is 60 degrees, and D is the excenter relative to side BC. The extension of line DC meets the circumcircle at point E. If DE is 10 units, find AD.
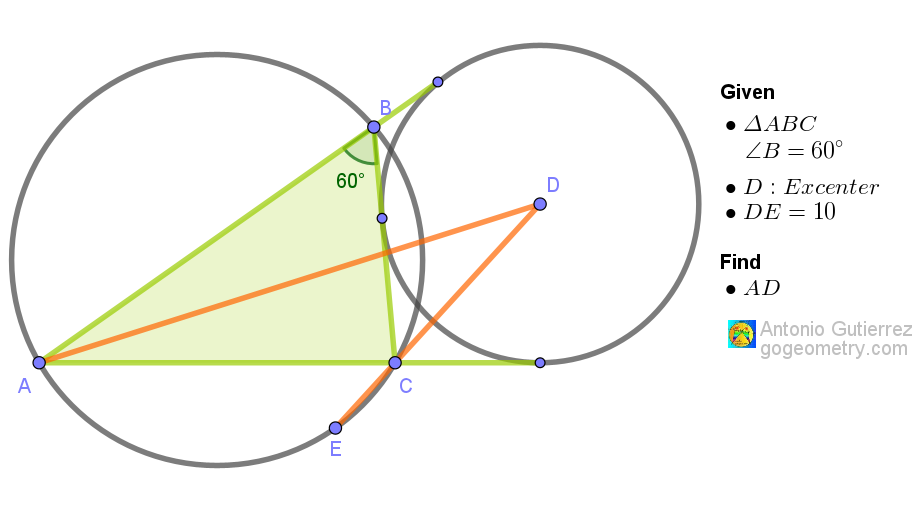
Excenter in place,
Circumcircle intersects,
Solve for AD's trace.
Uncover and share solutions to this problem.
Hints, Key Definitions and Descriptions
| Key Term | Definition |
|---|---|
| Triangle ABC | A triangle with vertices labeled A, B, and C. |
| Angle B | The angle formed at vertex B, given as 60 degrees. |
| Excenter (D) | A point located outside triangle ABC, serving as the center of the excircle opposite side BC. |
| Excircle | A circle outside triangle ABC, tangent to one of its sides and to the extensions of the other two sides. |
| Line DC | A line passing through excenter D and vertex C of triangle ABC. |
| Circumcircle | A circle that passes through all three vertices of triangle ABC. |
| Point E | The point where the extension of line DC intersects the circumcircle of triangle ABC. |
| Cyclic Quadrilateral | A quadrilateral whose vertices all lie on a single circle, called the circumcircle. |
| Segment DE | A line segment from point D (the excenter) to point E on the circumcircle, measuring 10 units. |
| Segment AD | The line segment from vertex A to excenter D, whose length needs to be determined. |
| Isosceles Triangle | A triangle with two sides of equal length. |
| Special Right Triangle 30-60 Degrees | A right triangle with angles measuring 30, 60, and 90 degrees, often featuring side lengths in the ratio 1:√3:2. |
| Auxiliary Line | A line added to a geometric figure to aid in solving a problem or proving a theorem. |
Flyer of problem 1580 using iPad Apps
Read more, explore further
Geometry Problems
Open Problems
Visual Index
All Problems
Triangle
Circle
60 degrees
30-60 Right Triangle
Cyclic Quadrilateral
Isosceles Triangle
View or Post a solution
Search our site with Google: