Geometry Problem 1566: Unlock the Proof: Demonstrate AC Equals AE + CD in an Equilateral Triangle ABC Involving Cevians and 60 Degrees.
Given an equilateral triangle ABC, the cevians AD and CE intersect at an angle of 60 degrees. Prove that the length of side AC is equal to the sum of the lengths of segments AE and CD.
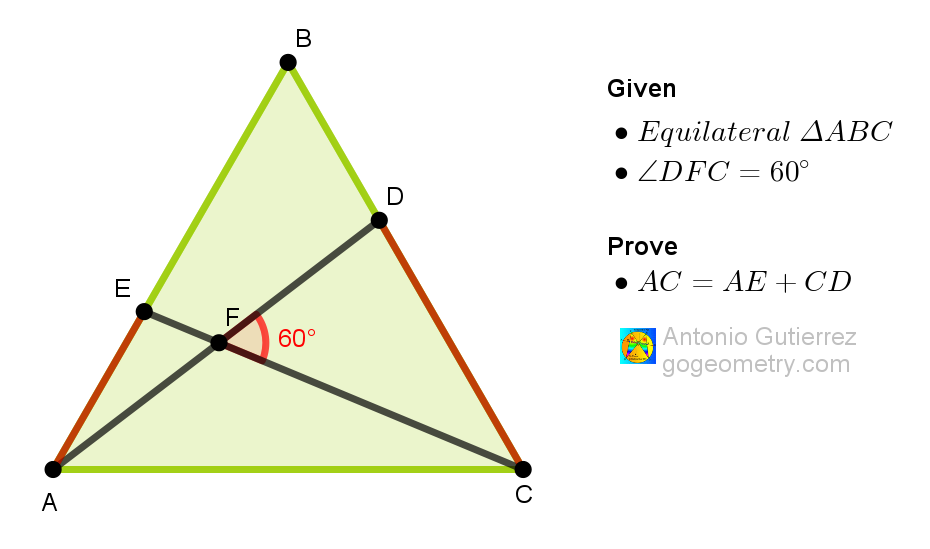
In equilateral,
Cevian paths converge bright,
AC's length unfolds.
Academic Levels: Suitable for High School and College Mathematics Education
Uncover and share solutions to this problem.
Key Definitions and Descriptions
| Key Definitions | Description |
|---|---|
| Equilateral Triangle | A triangle with all three sides of equal length and all three angles equal to 60 degrees. |
| Cevian | A line segment extending from a vertex of a triangle to the opposite side (or its extension). |
| Angle of 60 Degrees | The measure of the angle formed between cevians AD and CE in the equilateral triangle. |
| Side AC | The length of the side AC in the triangle, which needs to be proven as equal to the sum of the lengths of segments AE and CD. |
| Segments AE and CD | The lengths of segments AE and CD which, when added together, are to be proven equal to the length of side AC. |
Flyer of problem 1566 using iPad Apps
Read more, explore further
Geometry Problems
Open Problems
Visual Index
All Problems
Angles
Triangle
Equilateral Triangle
60-degrees
Angle Bisector
Cyclic Quadrilateral
View or Post a solution
Search our site with Google: