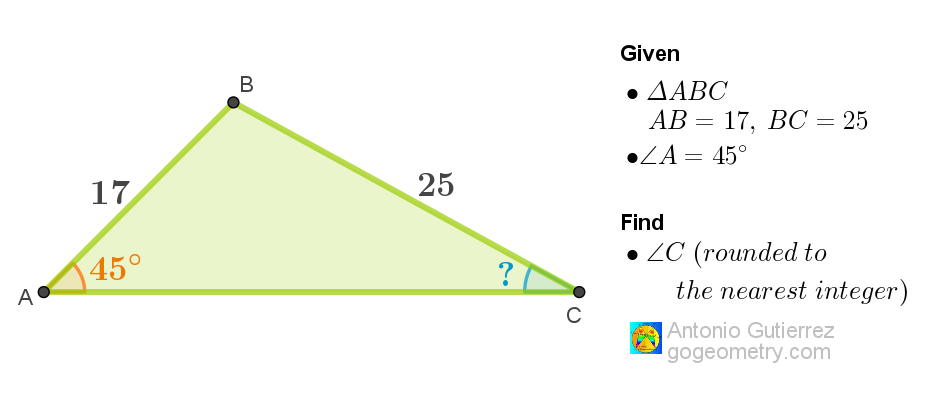
Geometry Problem 1572: Discover the Secrets of Triangle ABC: Calculate Angle C with Geometric Methods Using Sides AB=17, BC=25, and Angle A=45 Degrees. A High School and College Geometry Challenge

Given a triangle ABC, where AB=17, BC=25, and angle A=45 degrees, determine the measure of angle C rounded to the nearest integer. Please use geometric methods rather than trigonometry to enhance understanding of the triangle's properties.

Uncover and share solutions to this problem.

Key Definitions and Descriptions

Key Term	Description
Triangle ABC	A geometric figure consisting of three vertices (A, B, and C) connected by three sides (AB, BC, and AC).
AB	The side of the triangle between vertices A and B, with a length of 17 units.
BC	The side of the triangle between vertices B and C, with a length of 25 units.
Angle A	The angle formed between sides AB and AC, measuring 45 degrees.
Angle C	The angle opposite side AB, which is to be determined using geometric methods.
Geometric Methods	Approaches to solving the problem based on the properties of shapes and their relationships, rather than using trigonometric formulas.
Nearest Integer	The result of rounding the calculated measure of angle C to the closest whole number.

---

Flyer of problem 1572 using iPad Apps