Geometry Problem 1531: Discover How to Calculate the Length of a Chord in a Circle with Diameter Intersection and an Angle between the Diameter and Chord - A High School Challenge
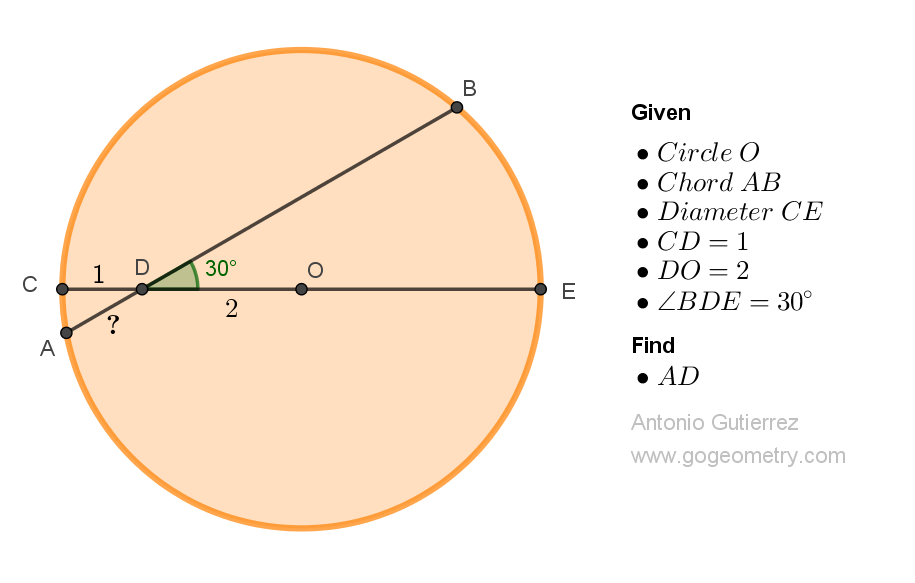
Consider a circle with center O. A chord AB intersects the diameter CE at point D, such that CD = 1, DO = 2, and angle BDE measures 30 degrees. Find the length of AD.
View or post a solution
Discover Even More: See Also...
Problem 1532
Problem 1530
Problem 1529
Problem 1528
Problem 1527
Problem 1526
Thematic Poem:
Chasing the Chord: A Pythagorean Tale of Discovery Within a Circle
Within a circle's curved embrace,
A chord cuts
through with angled grace,
Where diameter and chord
do meet,
A Pythagorean tale to complete.
A challenge set to find the length,
Of this chord,
with geometry's strength,
By applying the theorem's
might,
And revealing its hidden insight.
"Discover!" cries the eager mind,
To unravel this
puzzle designed,
To hone its skill with every try,
Until the answer draws nigh.
With steps and rules to guide the way,
The path to
solve now on display,
A journey that the curious
crave,
To find the chord they aim to save.
And when at last the chord is found,
A joyous
victory does resound,
For knowledge gained is a
treasure bright,
And with it, wisdom takes its
flight.
If you're interested in finding more poems with a focus on geometry, you may enjoy this collection: More geometry thematic poems.
Recent Additions
Geometry Problems
Open Problems
Visual Index
All Problems
Triangle
Circle
Chord
Angle
30-60 Right Triangle
Perpendicular lines
Right Triangle
View or Post a solution
Search our site with Google: