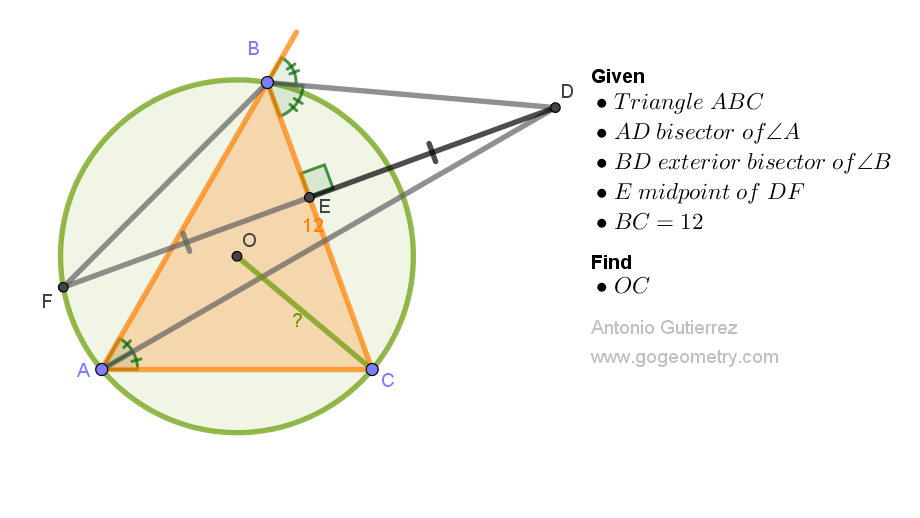
Clever Geometry Problem 1553: Solving for OC in Triangle ABC with Unique Angle Bisectors

In triangle ABC, the angle bisector of A and the exterior angle bisector of B meet at point D. From D, a perpendicular is drawn to BC, intersecting BC at E and the circumscribed circle with center O at F, where E is the midpoint of DF. Given that BC measures 12 units, the task is to find OC.

Illustration of problem 1553: Diagram of triangle ABC with angle bisectors, perpendiculars, and circumscribed circle centered at O

In triangle's heart,
Angles and bisectors meet,
D, the sacred point.
From O's center, truth we seek,
OC's length, math's mystique.

Uncover and share solutions to this problem.

Utilizing Conformal Maps in Geometric Art: Addressing Issue 1553

Geometric Art Utilizing Conformal Maps: Tackling Problem 1553

In the context of geometric art, a conformal map refers to a type of artistic representation or transformation that preserves angles between shapes, lines, or patterns. It involves mapping one geometric arrangement onto another while maintaining the relative angles between the elements.

Geometric artists often use conformal maps to create visually interesting and aesthetically pleasing artworks. These maps can distort shapes, but they do so while keeping the angles between lines or curves constant. This can lead to intricate and visually captivating designs that may appear intricate or surreal.