Geometry Problem 1577: Prove AB Equals BD Plus CD in Triangle ABC with Given Angles 20, 30, 40 Degrees and Congruent Segments. A High School and College Challenge

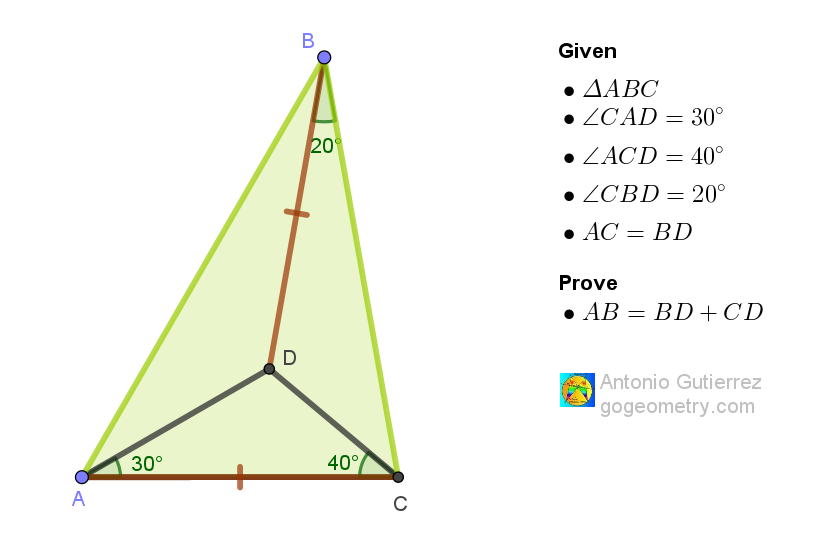
In triangle ABC, point D is inside the triangle. Given that angle CAD is 30 degrees, angle ACD is 40 degrees, angle CBD is 20 degrees, and segments AC and BD are congruent, prove that the length of segment AB equals the sum of the lengths of segments BD and CD.

Uncover and share solutions to this problem.

Key Definitions and Descriptions

Term	Description
Triangle ABC	A triangle named ABC, where D is an interior point. This triangle is central to solving the geometric problem presented.
Interior Point D	Point D is located inside triangle ABC. Its position relates to specific angle measures and segment congruences relevant to proving the problem's statement.
Angles CAD, ACD, CBD	These angles inside triangle ABC measure 30, 40, and 20 degrees respectively, influencing the geometric properties and relationships within the triangle.
Congruent Segments AC and BD	Segments AC and BD are of equal length, a key property used in the proof of the problem's statement.
Sum of the Lengths of Segments BD and CD	The problem requires proving that the length of segment AB is equal to the combined lengths of segments BD and CD.
Equilateral Triangle	A triangle where all three sides are of equal length and each angle measures 60 degrees. This term is general geometry knowledge, not directly applicable to this problem.
Isosceles Triangle	A triangle with at least two sides of equal length, which makes the angles opposite these sides also equal. This term is useful for understanding basic triangle properties.
Auxiliary Lines	Lines drawn in addition to the existing figure to aid in solving a problem or proving a theorem. These are often crucial in complex geometric proofs.

---

Flyer of problem 1577 using iPad Apps