Geometry Problem 1565: Find the Length of BF in Triangle ABC Involving Median, Perpendicular, Midpoint, and Congruence.

In triangle ABC, BD is a median, and AE is perpendicular to BD. Point F is on segment BE such that CF is congruent to AB. If DE = 5, find the length of BF.

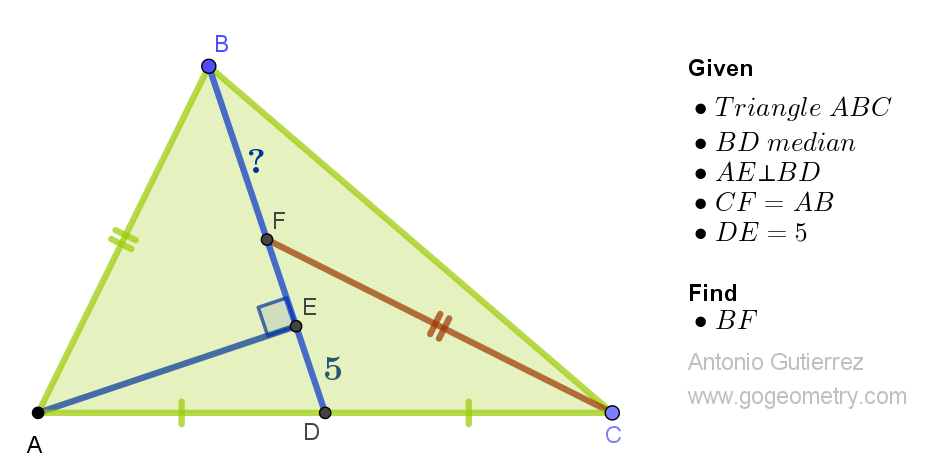
Diagram of triangle ABC Involving Triangle, Median, Perpendicular, Congruence. Geometry Problem 1565.

Median cuts in two,
Perpendicular splits a side more.
BF length remains veiled.

Academic Levels: Suitable for High School and College Mathematics Education

Uncover and share solutions to this problem.

Key Definitions and Descriptions

Vocabulary	Description
Triangle ABC	A triangle with vertices at points A, B, and C.
Median BD	A line segment from vertex B to the midpoint of the opposite side AC.
Perpendicular AE	A line segment from point A perpendicular to BD, intersecting BD at point E.
Point F	A point on segment BE such that CF is congruent (equal in length) to AB.
DE	The length of segment DE, which is given as 5 units.
BF	The length of segment BF, which is to be found.
Congruent	Having the same size and shape. In this context, CF is congruent to AB.