Geometry Problem 1569: Proving the Length of EG Equals the Diameter of the Incircle of Triangle BDE in Isosceles Triangle ABC with Inscribed Square CDEF. A High School and College Geometry Challenge
In an isosceles triangle ABC with AB=BC, a square CDEF is constructed with D on BC and E on AB. The side EF intersects AC at G. Prove that the length of EG equals the diameter of the incircle of triangle BDE.
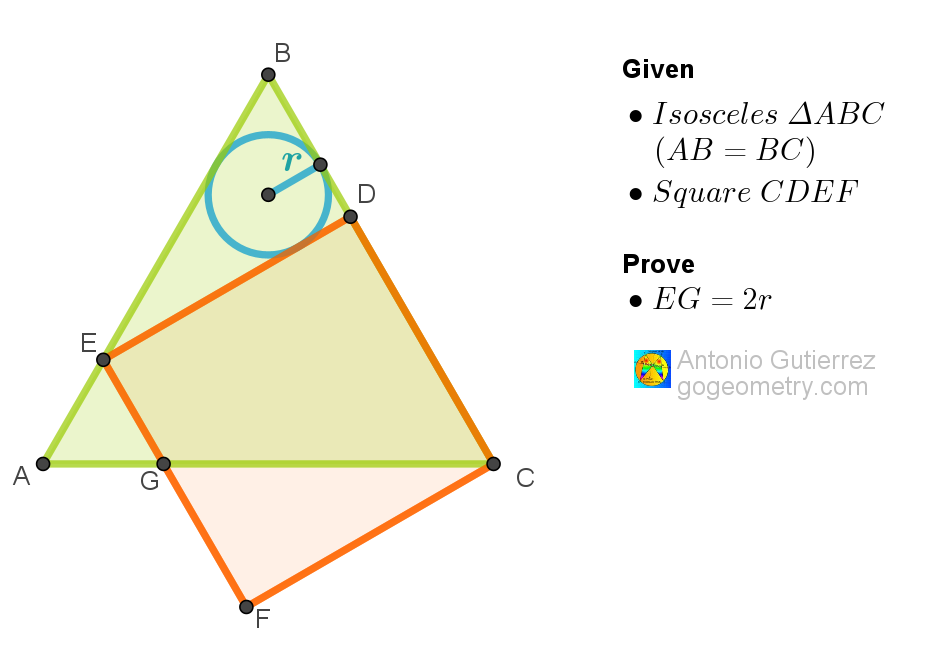
Square within triangle,
Intersecting lines reveal,
Circle's hidden truth.
Academic Levels: Suitable for High School and College Mathematics Education
Uncover and share solutions to this problem.
Key Definitions and Descriptions
| Vocabulary | Description |
|---|---|
| Isosceles Triangle | A triangle with two sides of equal length. |
| Isosceles Triangle ABC | An isosceles triangle where AB = BC. |
| Square CDEF | A square constructed such that vertex D lies on BC and vertex E lies on AB. |
| Point G | The intersection point of side EF of the square with AC of the triangle. |
| EG | The segment from E to G, which we need to prove is equal to the diameter of the incircle of triangle BDE. |
| Incircle | The largest circle that fits inside a triangle, touching all three sides. |
| Diameter of the Incircle | Twice the radius of the incircle, which is the circle inscribed within triangle BDE. |
Flyer of problem 1569 using iPad Apps

Read more, explore further
Geometry Problems
Open Problems
Visual Index
All Problems
Angles
Triangle
Isosceles Triangle
Right Triangle
Circle
Incircle
Diameter
Quadrilateral
Square
View or Post a solution
Search our site with Google: