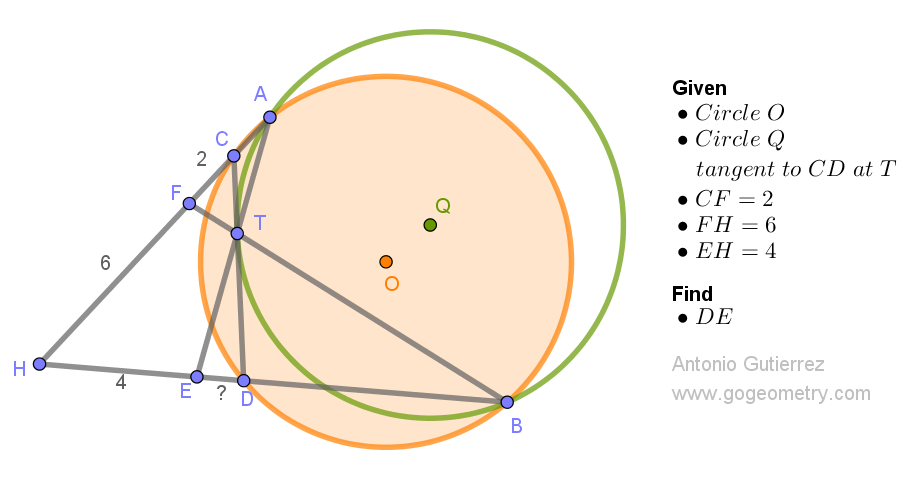
Geometry Problem 1555: Find Length of DE. The problem involves chords, tangent, circles, and intersections of line

Consider a circle with center O. As shown in the figure, we draw chord CD and an additional circle centered at Q, tangent to CD at point T, and intersecting the original circle at A and B. The extensions of lines AC and BD meet at H. Likewise, extensions of lines AT and BT intersect BH and AH at E and F. Given CF = 2, FH = 6, and EH = 4 units, find the length of DE.

Illustration of problem 1555: Circle with chord CD, tangent circle, and lines AC, BD, AT, BT, and points A, B, H, E, F.

In circle's embrace,
Chord and tangent interlace,
Figures intertwine,
Lines converge in graceful dance,
DE's length we seek, advance.

Uncover and share solutions to this problem.

Utilizing Stereographic Projection in Geometric Art: Addressing Issue 1555

Applying Stereographic Projection in Geometric Art: An Artistic Transformation of Issue 1555

In this illustration, stereographic projection and mathematical transformations are utilized to distort and reshape the geometry figure of problem 1554, producing distinctive spherical effects. This exemplifies an engaging application of geometry in digital image editing, empowering users to create visually captivating images from their figures.

Stereographic projection is a mathematical technique that maps points on a sphere to points on a plane (flat surface).