Geometry Problem 1576: Congruency of Segments in Triangle ABC with Angles 30 and 20 Degrees and an Interior Cevian. A High School and College Challenge

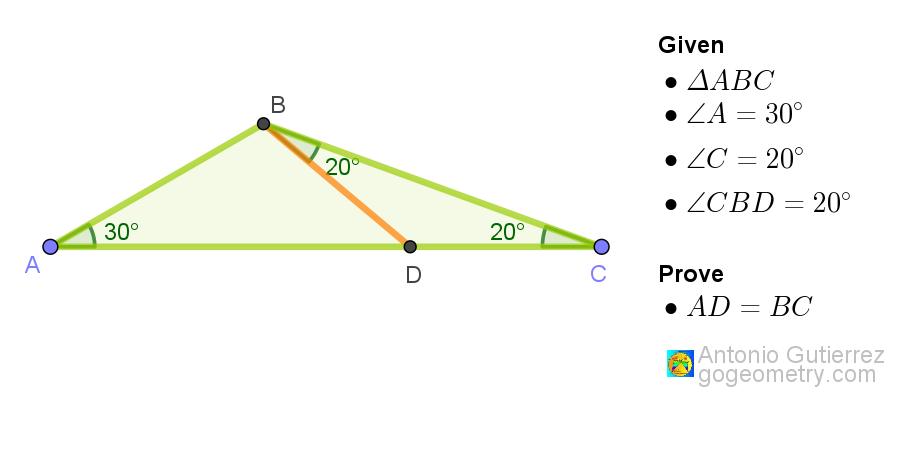
In triangle ABC, angles at A and C are 30 and 20 degrees, respectively. An interior cevian BD forms a 20-degree angle with BC. Prove that segments AD and BC are congruent.

Uncover and share solutions to this problem.

Key Definitions and Descriptions

Vocabulary	Description
Triangle ABC	A triangle where the angles at vertices A and C measure 30 degrees and 20 degrees, respectively.
Angle A	The angle at vertex A of triangle ABC, measuring 30 degrees.
Angle C	The angle at vertex C of triangle ABC, measuring 20 degrees.
Cevian BD	An interior line segment BD drawn from vertex B, intersecting side AC, forming a 20 degrees angle with side BC.
Angle with BC	The angle formed between cevian BD and side BC, which measures 20 degrees.
Congruent Segments	Segments AD and BC are to be proven congruent, meaning they are equal in length.

---

Flyer of problem 1576 using iPad Apps