Geometry Problem 1571: Prove that the intermediate angle in a Pythagorean Triple 7-24-25 measures 74 degrees using geometric methods. A High School and College Geometry Challenge
Given a Pythagorean triangle with sides measuring 7, 24, and 25, demonstrate that the intermediate angle, rounded to the nearest integer, measures 74 degrees. Please use geometric methods rather than trigonometry to enhance understanding of the triangle's properties.
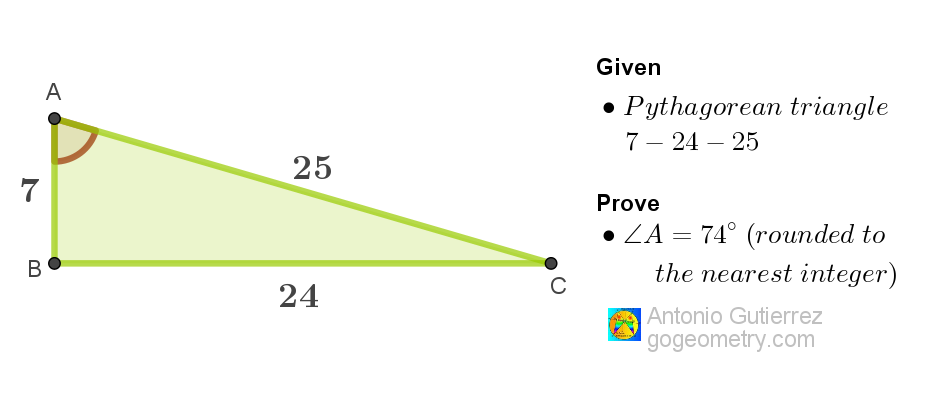
Pythagorean sides,
Seventy-four degrees found,
Geometry shines.
Uncover and share solutions to this problem.
Key Definitions and Descriptions
| Vocabulary | Description |
|---|---|
| Pythagorean Triple | A right-angled triangle where the sides are three positive integers such that satisfy the Pythagorean theorem.. In this problem, the sides are 7, 24, and 25. |
| Intermediate Angle | The angle in a triangle that is neither the largest nor the smallest. For the 7-24-25 triangle, this angle is being proven to be approximately 74 degrees. |
| Geometric Methods | Techniques used to solve problems based on the properties of shapes and figures, rather than using trigonometric functions. |
| Geometric Proof | A logical argument using definitions, axioms, and previously established theorems to show that a geometric statement is true. |
| High School and College Geometry | Courses and studies focusing on the properties and applications of shapes, sizes, and theorems in both high school and college-level math. |
Flyer of problem 1571 using iPad Apps

Read more, explore further
Geometry Problems
Open Problems
Visual Index
All Problems
Angles
Triangle
Right Triangle
Special Right Triangle 3-4-5
Angle Bisector
Angle Bisector Theorem
View or Post a solution
Search our site with Google: