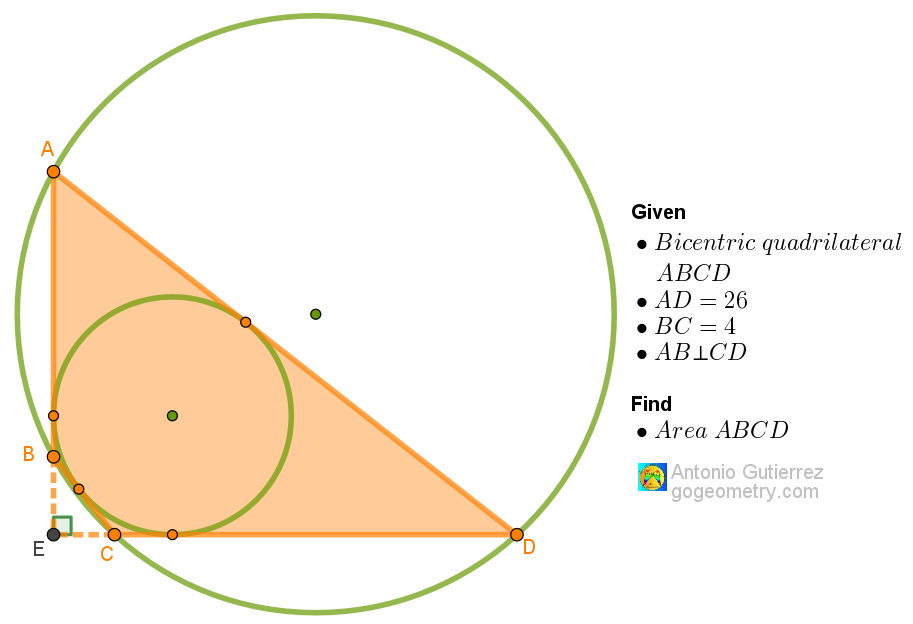
Geometry Problem 1578: Find the Area of a Bicentric Quadrilateral with Perpendicular Extensions of Opposite Sides! A High School and College Challenge

Determine the area of a bicentric quadrilateral where two opposite sides measure 25 units and 4 units, respectively, and the other two extended sides intersect perpendicularly.

Uncover and share solutions to this problem.

Hints, Key Definitions and Descriptions

Hints, Key Term	Description
Bicentric Quadrilateral	A quadrilateral that has both an inscribed circle and a circumscribed circle. Such a quadrilateral is both cyclic and tangential.
Inscribed Circle	A circle that touches all four sides of a quadrilateral from the inside. In a bicentric quadrilateral, this circle is perfectly tangent to each side.
Circumscribed Circle	A circle that passes through all four vertices of a quadrilateral. For a quadrilateral to be bicentric, it must also have an inscribed circle.
Cyclic Quadrilateral	A quadrilateral with all its vertices lying on a single circumscribed circle. Opposite angles of a cyclic quadrilateral sum to 180 degrees.
Tangential Quadrilateral	A quadrilateral that has an inscribed circle touching all four sides. In a bicentric quadrilateral, the sum of the lengths of opposite sides is equal.
Extended Sides	When the sides of a quadrilateral are prolonged beyond their endpoints. In this problem, two opposite sides are extended until they intersect perpendicularly.
Intersect Perpendicularly	The condition where two lines or sides meet at a 90 degrees angle. In this problem, the extended sides of the quadrilateral meet perpendicularly.
Area of Tangential Quadrilateral	The area of a tangential quadrilateral can be calculated by multiplying the inradius (the radius of the inscribed circle) by the semiperimeter (half the sum of all side lengths) of the quadrilateral.

---

Flyer of problem 1578 using iPad Apps