|
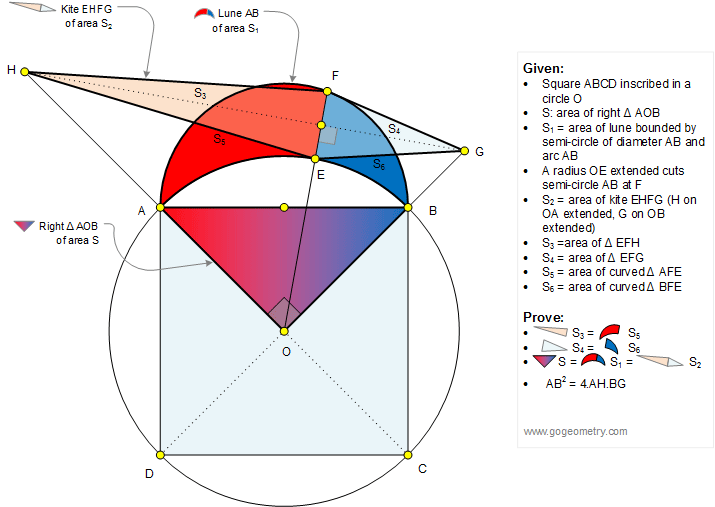
The figure shows a square ABCD
inscribed in a circle O. S is the area of the right triangle
AOB, S1 is the area of the lune of Hippocrates
bounded by the semi-circle of diameter AB and the arc AB. A
radius OE extended cuts semi-circle AB at F. S2 is
the area of the
kite EHFG (H on OA extended, G on OB extended). S3
and S4 are the areas of the triangles EFH and EFG,
respectively. S5 and S6 are the areas of
the curved triangles AFE and BFE.
Prove that (1) S3
= S5; (2) S4 = S6; (3) S = S1
= S2; (4) AB2 = 4.AH.BG.
This entry
contributed by Markus Heisss, Wurzburg, Bavaria. Published in:
"Die Wurzel - Zeitschrift fur Mathematik, Heft 11/2015",
www.wurzel.org.
|
Art of Geometry Problem 1335 using Mobile Apps. Circle
Patterns.
Geometric art is a form of art
based on the use and application of geometric figures. A
geometric figure is any set or combination of points,
lines, surfaces and solids. A mobile app or mobile
application software is a computer program designed to run
on smartphones and tablet computers.
Home
|
Search | Geometry
|
Problems |
All
Problems |
Open Problems
|
Visual Index
|
10 Problems
|
Art |
Ten problems: 1331-1340
|
Right Triangle Area
Circle
|
Semicircle
|
Lune Index
|
Kite
|
Square area |
Circular Sector |
Circular Segment
|
Common Chord
|
Geometric Art: Mobile Apps
| iPad
|
Email
Post or view a solution to the problem 1335
Last updated: May 7, 2017
|