Triangles: Theorems and Problems 22

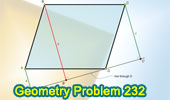Proposed Problem 232. Parallelogram, Line through a vertex, Perpendicular lines.  

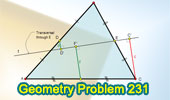Proposed Problem 231. Triangle, Midpoints, Transversal, Perpendicular lines.  

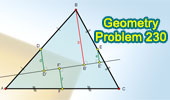Proposed Problem 230. Triangle, Midpoints, Transversal, Perpendicular lines.  

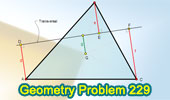Proposed Problem 229. Triangle, Centroid, Transversal, Perpendicular lines.  

Proposed Problem 228. Triangle, Midpoints, Exterior line, Perpendiculars lines.  

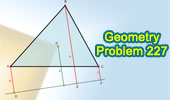Proposed Problem 227. Triangle, Centroid, Exterior line, Perpendicular lines.  

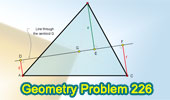Proposed Problem 226. Triangle, Centroid, Perpendiculars.  

Proposed Problem 224. Viviani's theorem, Isosceles triangle, Altitude, Distances, Point on the extension of the base.  

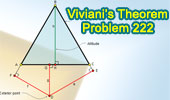
Proposed Problem 223. Viviani's theorem, Isosceles triangle, Altitude, Distances.  

Proposed Problem 222. Viviani's theorem, Equilateral triangle, Exterior point, Distances.  

Proposed Problem 221. Viviani's theorem, Equilateral triangle, Interior point, Distances.  

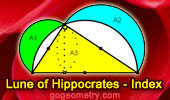Lune of Hippocrates Index.

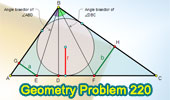Proposed Problem 220. Right Triangle, Altitude, Angle Bisector, Distance, Arithmetic Mean.

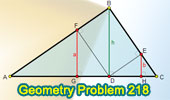Proposed Problem 218. Right triangle, Altitude and Projections.

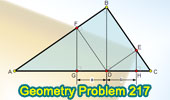Proposed Problem 217. Right triangle, Altitude and Projections.

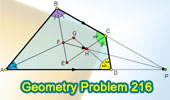Proposed Problem 216. Quadrilateral, Angle Bisectors, and Concurrency.

Journey to the Center of a Triangle (1976). Incenter, Circumcenter, Centroid, Orthocenter.

Congruent Triangles: SAS, SSS, ASA. Demonstrates with animation the various relationships of angles and sides to congruency in triangles.

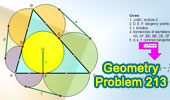Proposed Problem 213. Triangle, Incircle, Inradius, Semicircles, Common Tangents.

Proposed Problem 212. 120 Degree Triangle, Equilateral triangles, Areas.