Geometry Problem 1350: Triangle with three Intersecting Circles, Incircle, Collinear Points. Math, Tutoring,
Proposition
The figure below shows a triangle ABC with the incircle I. Circle A1 with a chord BC cuts circle I at A2 and A3. Circle B1 with a chord AC cuts circle I at B2 and B3. Circle C1 with a chord AB cuts circle I at C2 and C3. Lines A2A3 and BC meet at A4. Lines B2B3 and AC meet at B4. Lines C2C3 and BA meet at C4. Prove that C4, A4, and B4 are collinear.
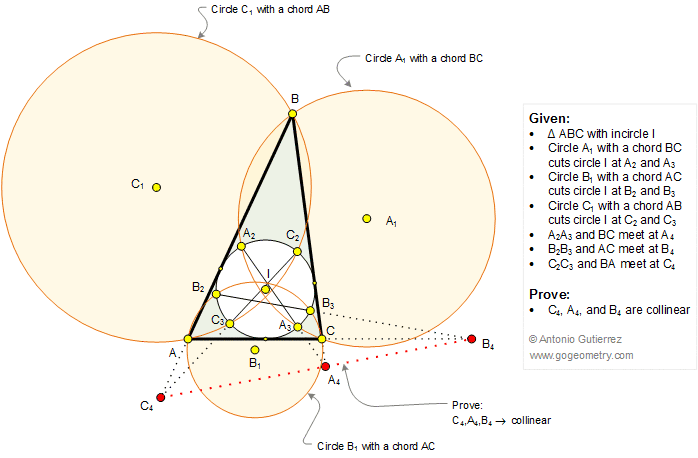
Sketch of problem 1350
Search gogeometry.com
Recent Additions
Geometry Problems
Ten problems: 1341-1350
Visual Index
Open Problems
All Problems
Triangles
Circle
Incircle
Chord
Intersecting Circles Index
Collinear Points
View or Post a solution