|
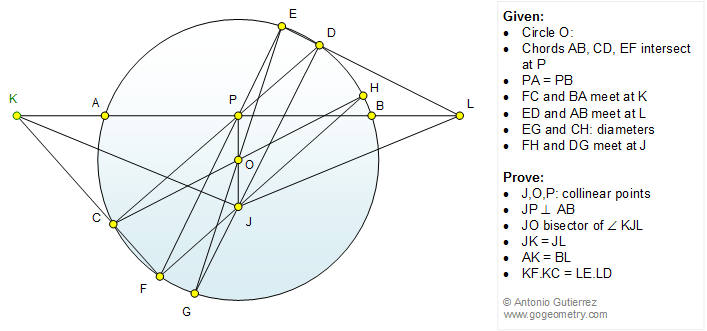
As illustrated, in a circle O, chords AB,
CD, and EF
intersect at P so that PA = PB. FC and BA extended meet at K. ED
and AB extended meet at L. EG and CH are diameters and FH and DG
meet at J. Prove that (1) J, O, and P are collinear points; (2)
JP is perpendicular to AB; (3) JO is the bisector of angle KJL;
(4) JK = JL; (5) AK = BL; (6) KF.KC = LE.LD
See also:
Art
work of problem 1191.
|

