 |
|
Online Geometry Problem 1077: Chain of Equal Tangent
Circles, Circular Sector, Area, Sangaku, Sacred Geometry. Level: High School, Honors Geometry, College, Mathematics Education
< PREVIOUS PROBLEM |
NEXT PROBLEM >
|
|
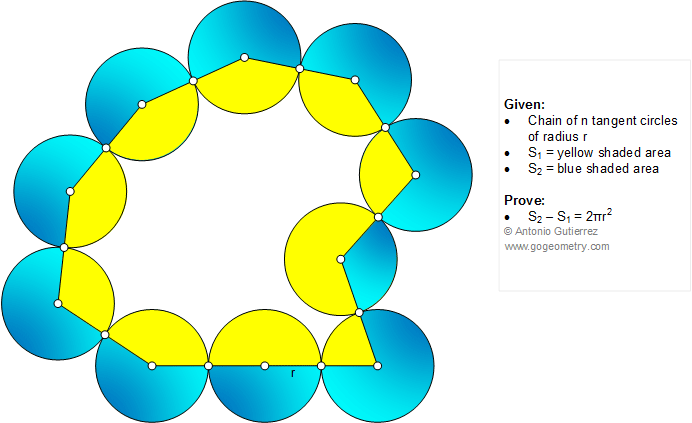
The figure shows a chain of n equal tangent
circles of radius r. If S1 is the area of yellow
shaded region and S2 is the area of blue shaded
region, prove that S2 - S1 = 2πr2
.
|
|
References:
|
|
  |
Reference: Fukagawa Hidetoshi, Tony Rothman,
Sacred Mathematics: Japanese Temple Geometry
(Princenton
University Press, 2008).
Between the seventeenth and nineteenth centuries Japan was totally isolated from the West by imperial decree. During that time, a unique brand of homegrown mathematics flourished, one that was completely uninfluenced by developments in Western mathematics. People from all walks of life—samurai, farmers, and merchants—inscribed a wide variety of geometry problems on wooden tablets called sangaku and hung them in Buddhist temples and Shinto shrines throughout Japan. |
|
|
|
|
|
|
 |
|