Infographic Geometry Problem 1061: Triangle, Inradius (r), Circumradius (R), Circumcircle, Angle Bisector, Distance from a point to a Line, Perpendicular. Level: High School, SAT Prep, College, Mathematics Education

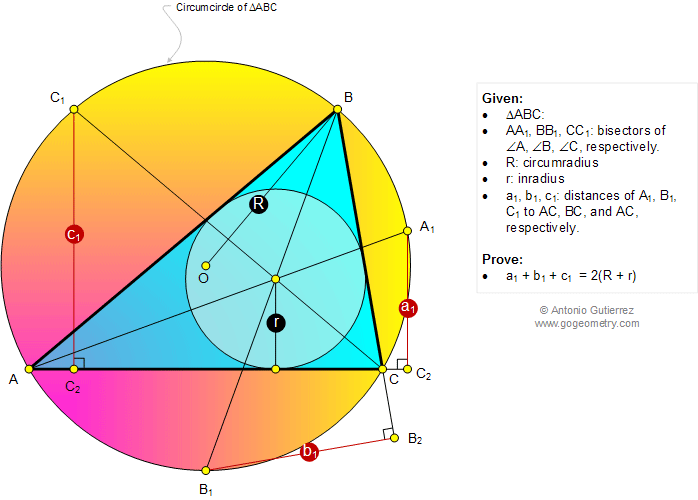
In a triangle ABC of inradius r and circumradius R (see the figure below), the bisectors of angles A, B, and C meet the circumcircle O at A₁, B₁, and C₁, respectively. If the distance of A₁, B₁, and C₁ to AC, BC, and AC, respectively, are a₁, b₁, and c₁, respectively, prove that a₁ + b₁ + c₁ = 2.(R + r).