|
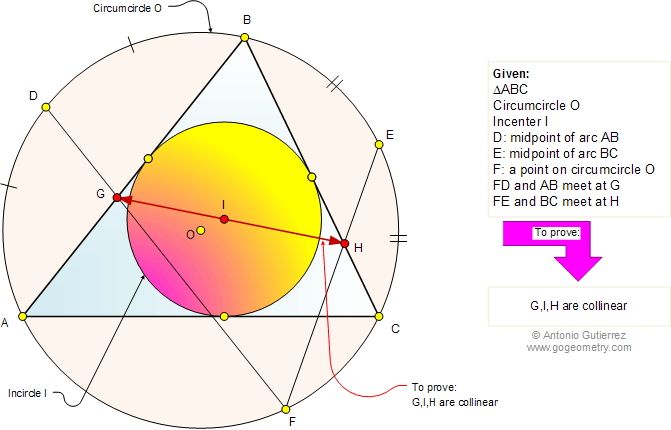
The figure shows a triangle ABC
with the circumcircle O and incenter I. D and E are the
midpoints of the arcs AB and BC, respectively. F is a point on
the circumcircle O, FD and AB meet at G, FE and BC meet at H.
Prove that points G, I, and H are collinear. See also:
Artwork
of Problem
669
|