Home
Geometry
Problems
All Problems
Cyclic Quadrilateral
331-340
Parallel
Chords
View or post a solution
|
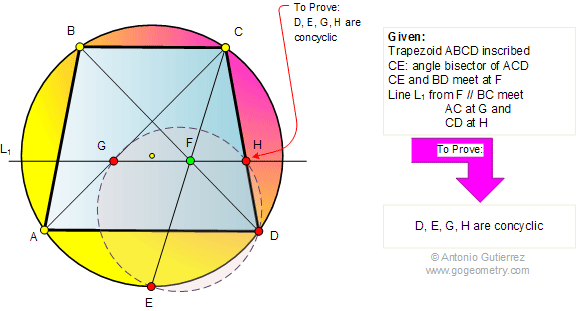
Problem 337. Isosceles Trapezoid, Angle bisector, Parallel, Concyclic points.
Level: High School, College, SAT Prep.
The figure shows an isosceles
trapezoid ABCD (AD // BC) inscribed in a circle. CE is the angle bisector of
angle ACD. CE meet BD at F. A line L1 from F is parallel to BC and meets AC
at G and CD at H.
Prove that points D, E, G, and H are concyclic. .
|
Recent Additions
|