|
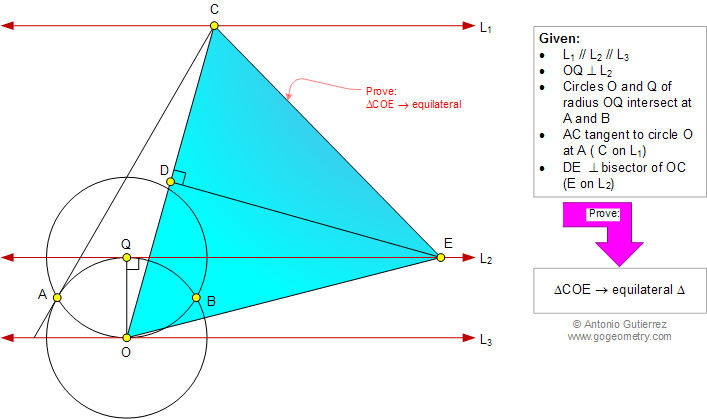
Lines L1, L2, and L3 are parallel
(Figure below) with OQ perpendicular to L2 (O on L3 and Q
on L2). Circles O and Q with radius OQ intersect at A and B. AC
is tangent to circle O at A (C on L1). DE is the perpendicular
bisector of OC (E on L2). Prove that triangle COE is
equilateral.
|