Online Geometry Problem 841: Triangle, Medians, Centroid, Circumcenters, Perpendicular, Congruence, Similarity. Level: High School, SAT Prep, College, Mathematics Education

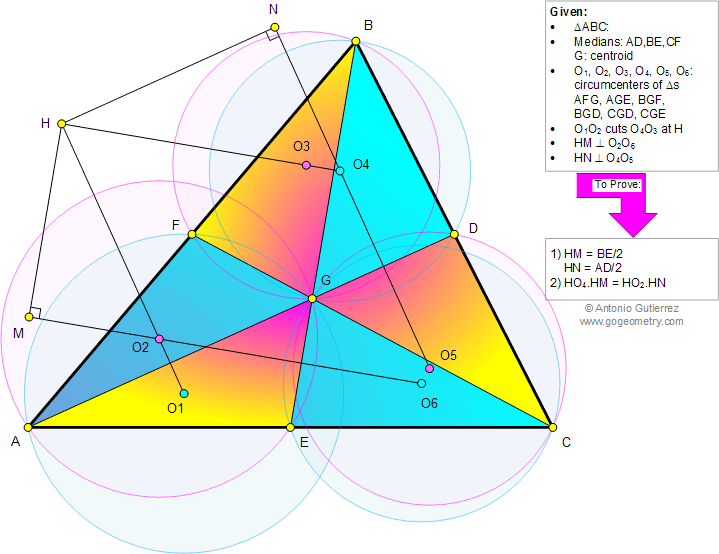
The figure below shows a triangle ABC, medians AD, BE,CF, and centroid G. O₁, O₂, O₃, O₄, O₅, O₆, are the circumcenters of triangles AFG, AGE, BGF, BGD, CGD, and CGE, respectively. O₁O₂ cuts O₄O₃ at H. HM is perpendicular to O₂O₆ and HN is perpendicular to O₄O₅. Prove that (1) HM = BE/2, HN = AD/2; (2) HO₄.HM = HO₂.HN