Geometry Problem 1512: Finding the Length of a Segment in a Triangle with a Median and a Cevian with Given Ratio. Difficulty Level: High School.
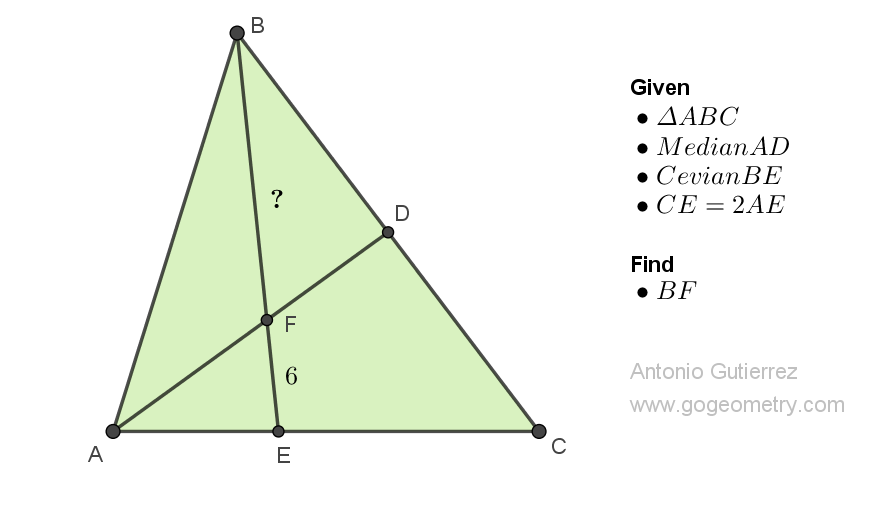
In a triangle ABC, AD is a median, and E is a point on AC such that CE = 2AE. AD and BE intersect at F. If EF measures 6 units, find the length of BF in units.
Definitions and Suggestions
- A triangle is a polygon that has three sides, three vertices, and three angles. Triangles are some of the most basic shapes in geometry and can be found in many different forms.
- A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side.
- A cevian is a line segment that connects a vertex of a triangle to the opposite side (or its extension).
- A given ratio of segments refers to the comparison of the lengths of two or more line segments in a specific ratio. Given ratios of segments can be used to solve problems related to scaling, similarity, and proportionality, among other things.
- The Midsegment Theorem, also known as the Midline Theorem or the Base Midsegment Theorem states that the length of the midsegment of a triangle is equal to half the length of the third side of the triangle.
Thematic Poem: Triangle, Median, Given Ratio
In geometry class, we learn of shapes
And how to measure all their
gapes
Triangles, with angles three
And sides to calculate, oh gee!
A problem posed, with median and cevian
To find the segment's
length, we're cravin'
With a given ratio of one to two
Our minds
race with what to do
With ruler and compass, we draw
The
lines we need, without a flaw
Then use the theorems we've been taught
To find the length, as we ought
We calculate and solve the
equation
Our hearts race with anticipation
And finally, we reach
the solution
A feeling of pride, a grand conclusion
In
geometry, we find our way
Using logic and reason every day
And
though the problems may be tough
We persevere, and that's enough.