Geometry Problem 1505: Parallel Rays, Angles, and Bisector. Difficulty Level: High School.
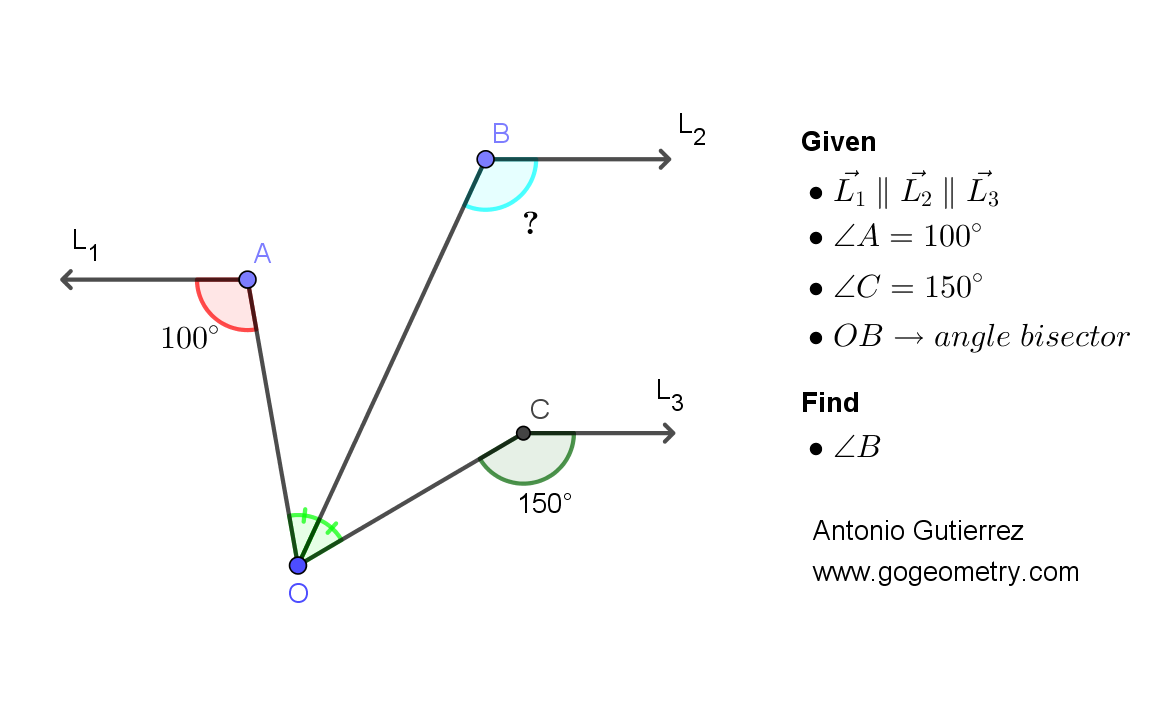
Given the figure with parallel rays L1, L2, and L3, and with angle A measuring 100 degrees and angle C measuring 150 degrees, find the measure of angle B, where OB is the bisector of angle AOC.
Definitions and Suggestions
- A ray is a straight line with a single endpoint that extends infinitely in one direction.
- An angle is a figure formed by two rays, or half-lines, that have a common endpoint and extend in different directions.
- An angle bisector is a line, segment, or ray that divides an angle into two equal parts. The line that divides the angle into two equal parts is called the bisector of the angle.
- Parallel lines are two lines in a plane that never meet or intersect, no matter how far they are extended.
- Suggestion:
Corresponding angles are angles that have the same relative position in each figure. When two lines are parallel, the corresponding angles are equal in measure.
If two lines are parallel, then the alternate interior angles formed by a transversal line cutting across the two lines are congruent.
If two lines are parallel, then the conjugate interior angles formed by a transversal line cutting across the two lines are supplementary, meaning that their measures add up to 180 degrees.