Geometry Problem 1502: The Geometric Intricacies of a Right Triangle's Incircle, Inradii and Tangential Quadrilateral

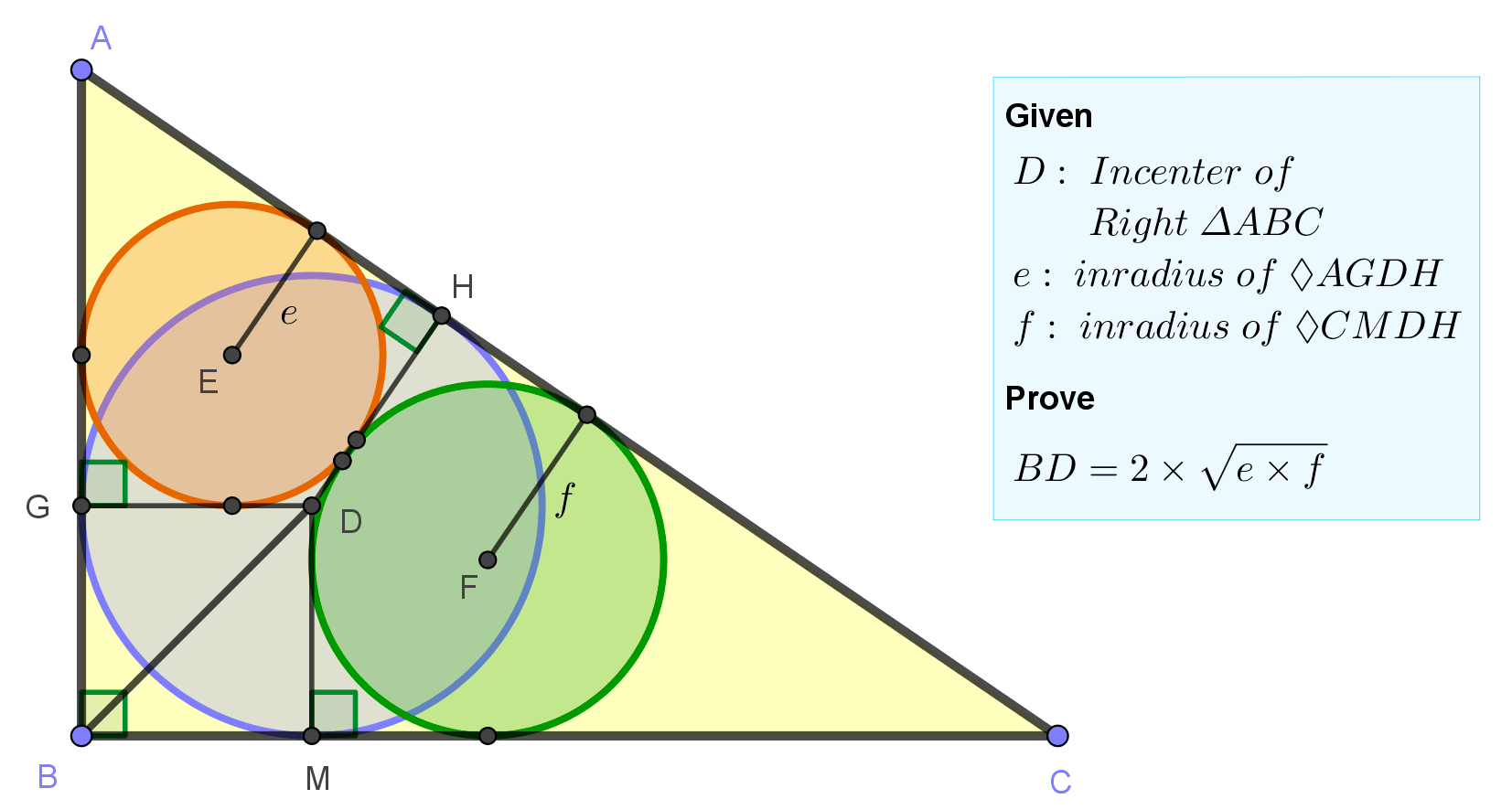
In the figure, D is the incenter of right triangle ABC, \(e\) and \(f\) are the inradii of the tangential quadrilaterals AGDH and CMDH, respectively. Prove that \(BD=2\cdot\sqrt {e\cdot f}\)

Incenter D sits,
Geometric means connect us,
Proof in right triangle.

Definitions

• Inradius (plural inradii) is the radius of an incircle.
• Incircle is a circle inscribed within another shape touching every side of it at one point.
• Incenter is the center point of an incircle.
• Tangential quadrilateral is a convex quadrilateral whose sides all can be tangent to an incircle

View solution