Dynamic Geometry Problem 1445: Van Aubel's theorem, Quadrilateral and Four Squares
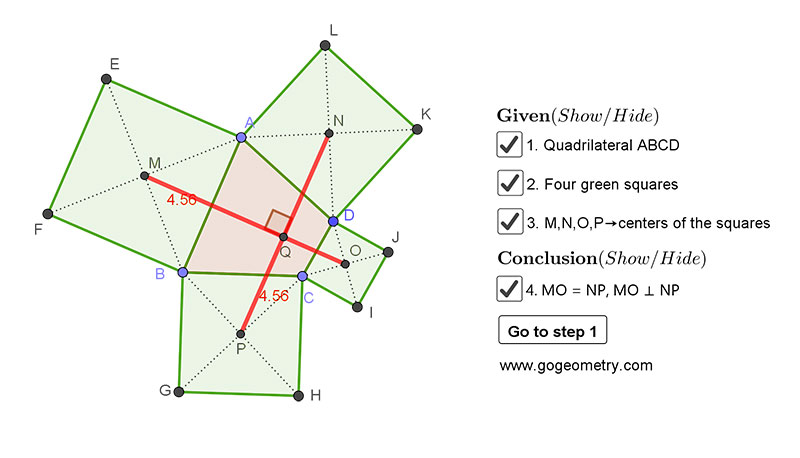
Given a quadrilateral ABCD and the squares constructed externally on each side, then the two line segments between the centers of opposite squares are congruent and are perpendicular.
Static Diagram of Van Aubel's Theorem
Poster of Problem 1445 using iPad Apps

Search gogeometry.com
Classroom Resource:
Interactive step-by-step animation using GeoGebra
This step-by-step interactive illustration was created with GeoGebra.
- To explore (show / hide): click/tap a check box.
- To stop/play the animation: click/tap the icon in the lower left corner.
- To go to first step: click/tap the "Go to step 1" button.
- To manipulate the interactive figure: click/tap and drag the blue points or figures.
GeoGebra is free and multi-platform dynamic mathematics software for all levels of education that joins geometry, algebra, tables, graphing, statistics and calculus application, intended for teachers and students. Many parts of GeoGebra have been ported to HTML5.
Recent Additions
Geometry Problems
Open Problems
Visual Index
Ten problems: 1411-1420
All Problems
Quadrilateral
Square
Triangle
Perpendicular lines
Congruence
Classical Theorems
Dynamic Geometry
van Aubel's theorem proof
GeoGebra
HTML5 and Dynamic Geometry
iPad Apps
View or Post a solution