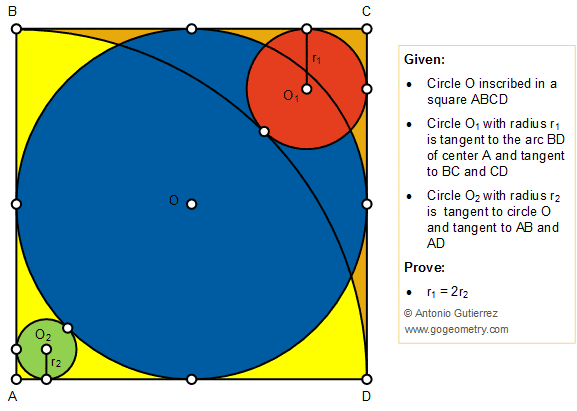
Geometry Problem 1427: Circle inscribed in a square, Arc, Tangent Line, Tangent Circles, Radii
A circle O is inscribed in a square ABCD. As shown in the figure below, a circle O1 with radius r1
is tangent to the arc BD of center A and
tangent to BC and CD. A circle O2
with radius r2 is tangent to circle O and tangent to AB and AD. Prove that r1 = 2r2.
Geometric Art of Problem 1427: Sketching, Typography, iPad Apps
Animation of the Conformal Mapping or Transformation of Problem 1427
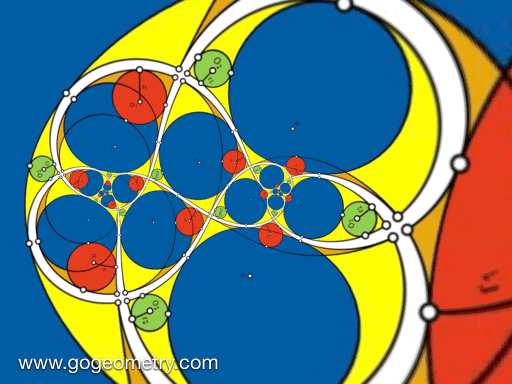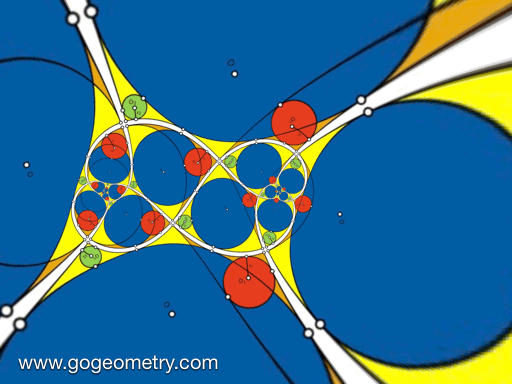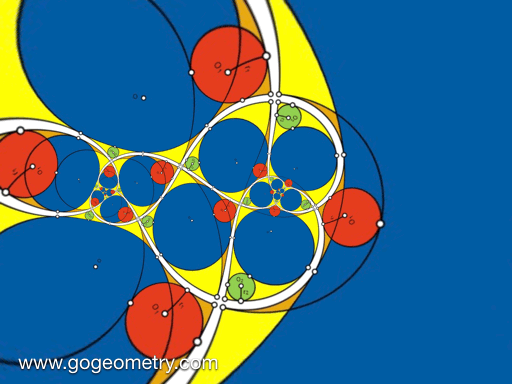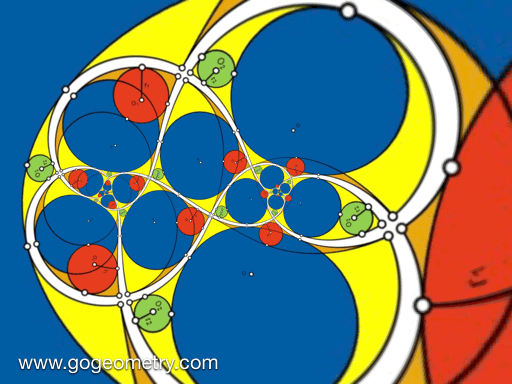
Conformal Mapping
A conformal mapping or conformal transformation is a continuous mapping preserving the form of infinitesimal figures. This conformal map produces a realistic view of the original image or map. This the conformal transformation of problem1427
See also: Typography and poster of problem 1426.
Search gogeometry.com
Recent Additions
Geometry Problems
Ten problems: 1411-1420
Visual Index
Open Problems
All Problems
Square
Circle
Tangent Circles
Tangent Line
Circle Inscribed in a Square
View or Post a solution
