Proposition

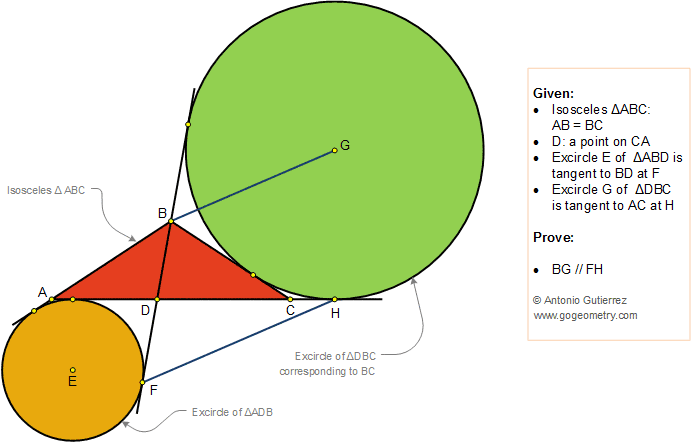
In the figure below, ABC is an isosceles triangle (AB = BC) and D is a point on AC. The excircle E of the triangle ABD corresponding to AD is tangent to BD extended at F. The excircle G of the triangle DBC corresponding to BC is tangent to AC extended at H. Prove that BG and FH are parallel.

BD is called an interior cevian of triangle ABC.
 

See solution below