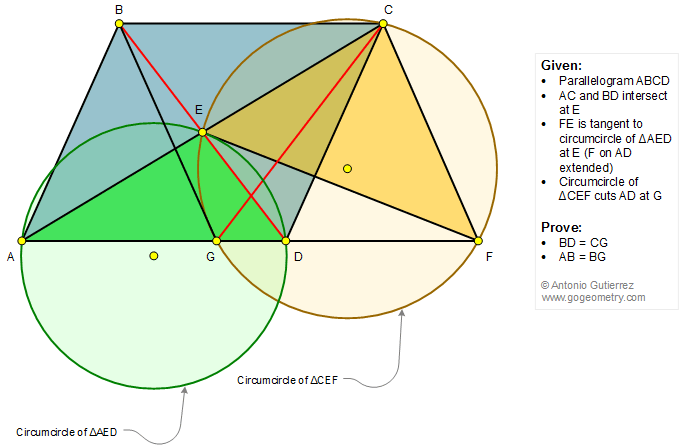
Geometry Problem 1337: Parallelogram, Diagonals, Circle, Circumcircle, Tangent Line, Triangle, Congruence. Math Infographic

In a parallelogram ABCD, diagonals AC and BD intersect at E. FE is tangent to the circumcircle of triangle AED at E, F lies on AD extended, as in the figure. The circumcircle of triangle CEF cuts AD at G. Prove that (1) BD = CG; (2) AB = BG.

Geometry Problem 1337: Parallelogram, Diagonals, Circle, Circumcircle, Tangent Line, Triangle, Congruence, Tutoring. Math Infographic