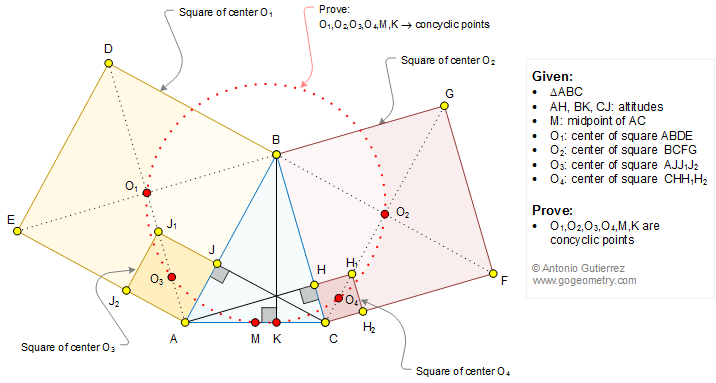
Geometry Problem 1294: Triangle, Altitudes, Four Squares, Center, Midpoint, Concyclic Points
The figure below shows a triangle ABC with the altitudes AH, BK, and CJ. O1, O2, O3, and O4 are the centers of the squares ABDE, BCFG, AJJ1J2, and CHH1H2, respectively. M is the midpoint of AC. Prove that the points O1, O2, O3, O4, M, and K are concyclic.