|
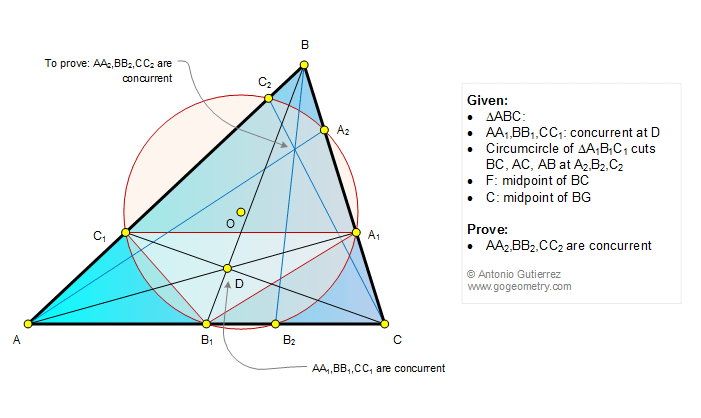
In a triangle ABC, the cevians AA1,
BB1, and CC1 are concurrent at D (see figure below).
The circumcircle of the triangle A1B1C1
cuts BC, AC, and AB at A2, B2, and C2,
respectively. Prove that the cevians AA2, BB2,
and CC2 are concurrent.
Geometry Problem 1233 in Motion
Click on the figure below.
|

