|
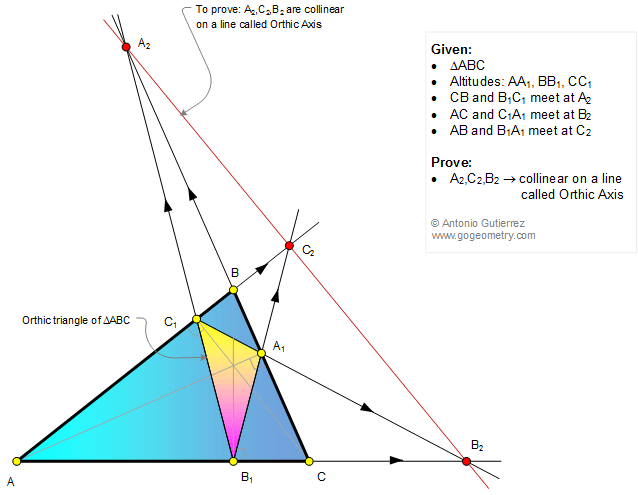
The figure shows a triangle ABC with the
altitudes AA1, BB1, and CC1. CB and B1C1
extended meet at A2, AC and C1A1
extended meet at B2,
AB and B1A1 extended meet at C2.
Prove that points A2, C2, and B2
are collinear on a line called Orthic Axes.
Note: The triangle A1B1C1
is called the orthic triangle of the triangle ABC.
Geometry Problem 1232 in Motion
Click on the figure below.
|

