|
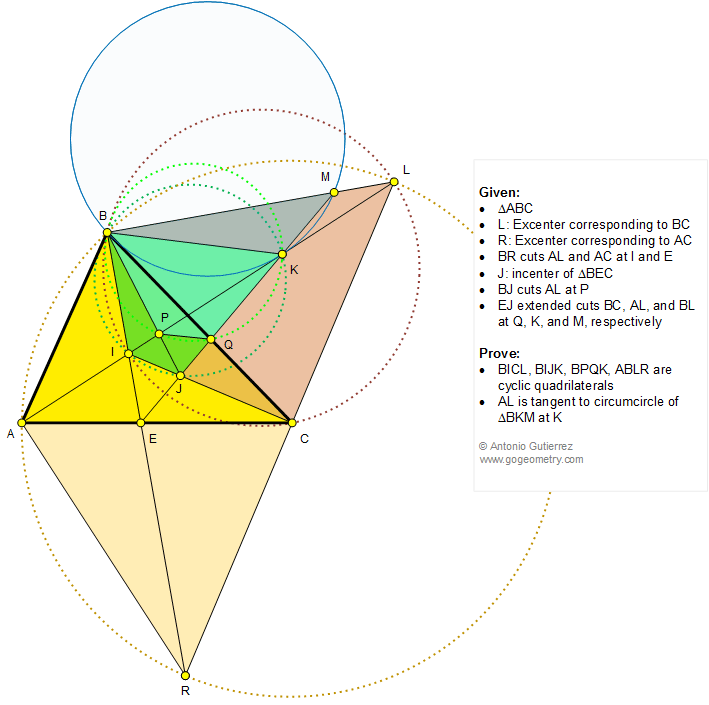
In a triangle ABC (see the figure), L and R are the excenters corresponding to BC and AC, respectively. BR cuts AL
and AC at I and E, respectively. J is the incenter of triangle
BEC. BJ cuts AL at P and EJ extended cuts BC, AL, and BL at Q, K, and M,
respectively. Prove that (1) BICL, BIJK, BPQK, and ABLR are
cyclic quadrilaterals; (2) AL is tangent to circumcircle of
triangle BKM at T.
This entry contributed by Sumith Peiris, Moratuwa, Sri Lanka.
|

