|
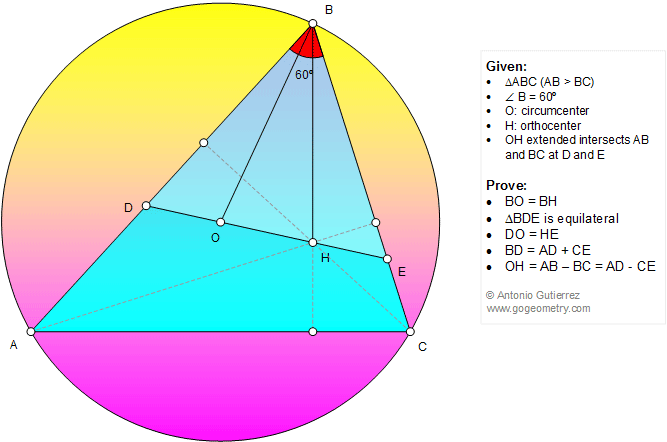
The figure below shows a triangle ABC
(AB > BC) with orthocenter H and circumcenter O such that angle
ABC = 60 degrees. Line OH extended intersects AB and BC at D and E, respectively. Prove that
(1) BO = BH, (2) triangle BDE is equilateral, (3) DO = HE, (4) BD = AD + CE,
(5) OH = AB - BC = AD - CE.
See
Geometry art of problem 1161
|