|
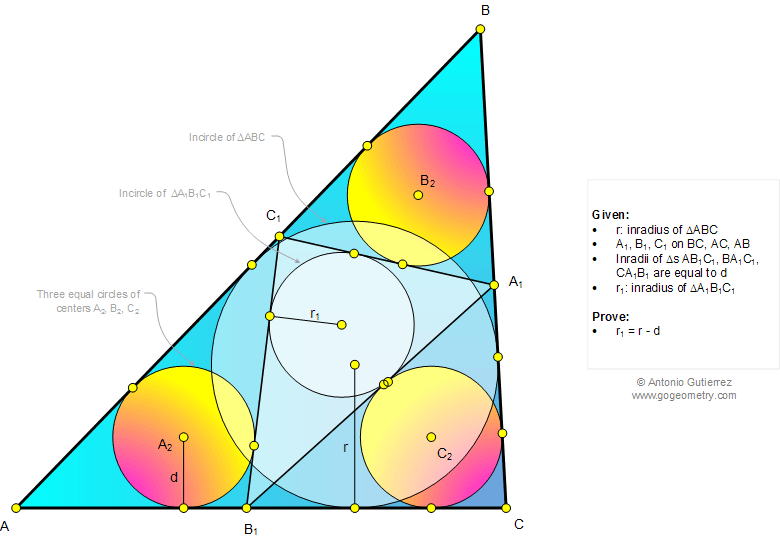
The figure below depicts triangle ABC, with points
A1, B1, and C1 located on BC, AC, and AB, respectively.
These points are chosen such that the inradii of triangles AB1C1, BA1C1, and
CA1B1 are all equal to d.
Let r represent the inradius of triangle ABC, and r1 denote the inradius of triangle
A1B1C1.
Prove that r1 = r - d.
The power of proof shines,
Inradius code revealed,
Triangles aligned.
School, college minds engage,
Unveiling truths on the page.
|
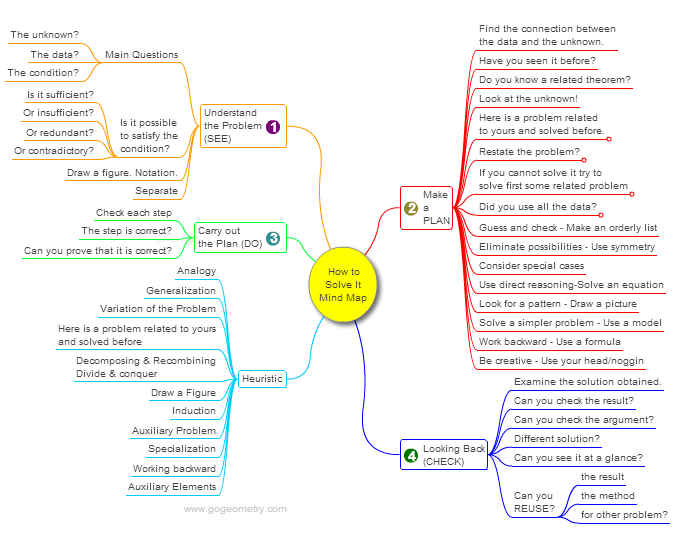
Mind Map: George P�lya's 1945 book,
"How to Solve It"
George P�lya's 1945 book "How to Solve It, A new aspect of
Mathematical Method", is a book describing methods of problem
solving. It suggests the following steps when solving a
mathematical problem: (1) First, you have to understand the
problem. (2) After understanding, then make a plan. (3) Carry
out the plan. (4) Look back on your work. How could it be
better?
A mind map is a diagram used to visually organize information, knowledge, concepts or ideas.
Home
|
Search | Geometry
|
Problems |
All
Problems |
Open Problems
|
Visual Index
|
10 Problems
|
Problems Art Gallery
| Art |
1031-1040
|
Triangle
|
Circle
|
Incircle
|
Areas
|
Triangle area
|
Perimeter
|
Tangent Line
|
Email
|
by Antonio Gutierrez
Add a solution to the problem 1037
Last updated: Sep 19, 2014
|

