How to Master Right Triangle Math: Beyond the Pythagorean Theorem
Comprehensive coverage of right triangle formulas, including the Pythagorean theorem, catheti, hypotenuse, altitude, projection, inradius, circumradius, exradius, semiperimeter, area, special right triangles, Poncelet's theorem, general extensions, and 3-D geometry.
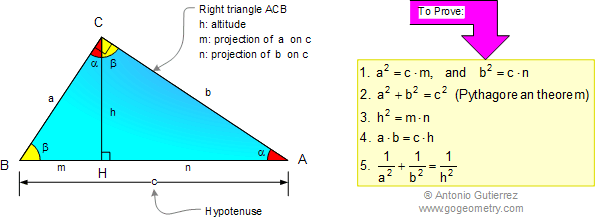
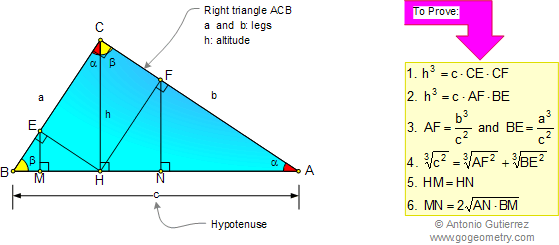
Pythagorean Theorem, Geometric Mean, and Projections
Proofs that use similarity and relationships between the sides of a right triangle.
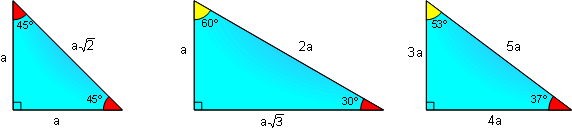
Special Right Triangles
Isosceles 45-45, 30-60, and the 3-4-5 triangle (angles 37-53 degrees).
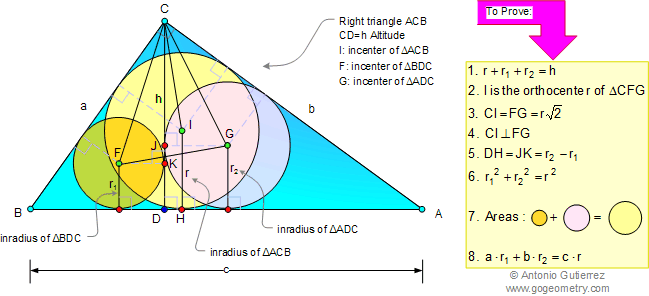
Centers and Radii: Incenter, Circumcenter, Orthocenter, Centroid
Sagitta: The distance between the midpoint of an arc and the midpoint of its chord.
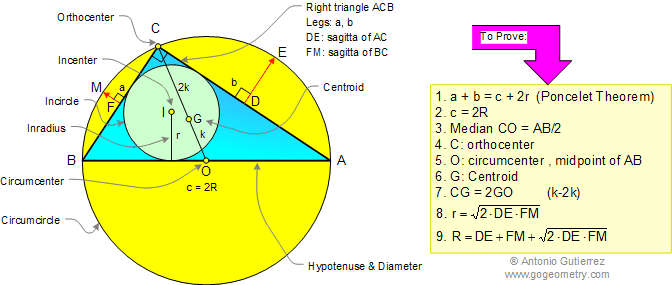
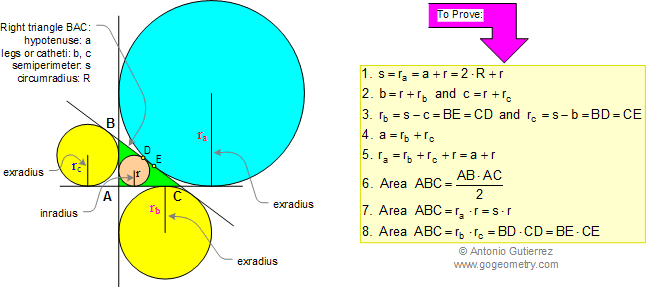
Inradius, Exradii, and Area Relations
Relations between inradius, exradii, semiperimeter, and area of a right triangle.
Orthogonal Projections
Using projections to derive relationships between catheti and hypotenuse.
Altitude, Inradii, and Area Relationships
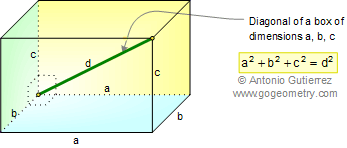
Diagonal of a Box: The 3D Extension of Pythagoras
Distance in Cartesian Coordinates
The Pythagorean theorem allows us to compute the straight-line distance between any two points with known coordinates.

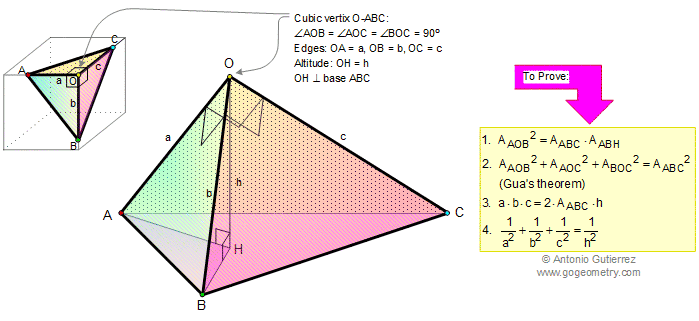
Pythagorean Theorem in 3D (De Gua’s Theorem)
In any tetrahedron with a cubic vertex O-ABC, the square of the area of the face opposite the cubic vertex is equal to the sum of the squares of the areas of the other three faces.
The Pythagorean Curiosity
Explore triangles and squares — fifteen conclusions in this fascinating extension of Pythagoras' ideas.

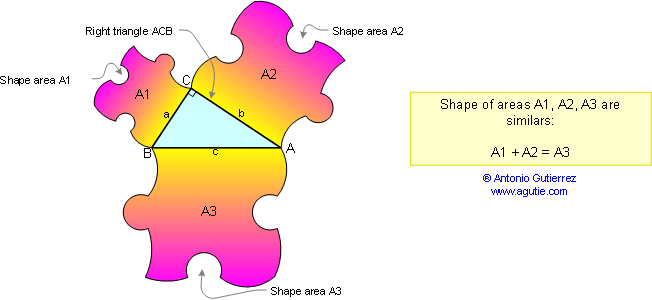
The General Extension of Pythagoras’ Theorem
If any three similar shapes are drawn on the sides of a right triangle, the area of the shape on the hypotenuse equals the sum of the areas on the other two sides.