Geometry Problem 884: The Pythagorean Curiosity, Fifteen Conclusions. Level: High School, Honors Geometry, College, Mathematics Education.

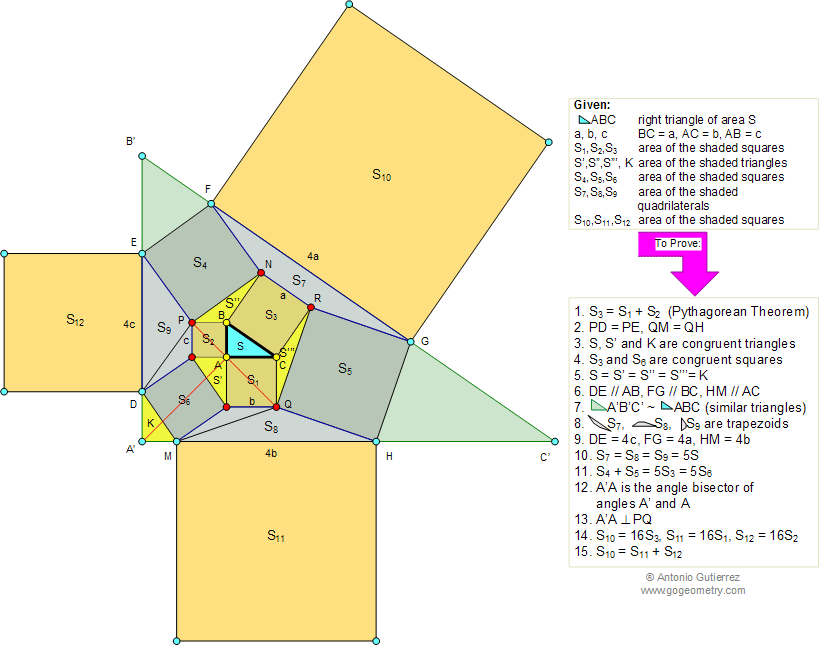
In the figure below, given a right triangle ABC of area S, BC = a, AC = b, AB = c. S₁, S₂, S₃ are the areas of the shaded squares built on the catheti (legs) b, c and the hypotenuse a, respectively. S₄, S₅, S₆ are the areas of the shaded squares. S₇, S₈, S₉ are the areas of the shaded quadrilaterals, S₁₀, S₁₁, S₁₂ are the areas of the shaded squares built on the lines FG, HM, DE, respectively. S', S'', S''', K are the areas of the shaded triangles. Prove the 15 conclusions below:

Reference: Loomis, Elisha Scott. The Pythagorean Proposition, Classics in Mathematics Education Series. National Council of Teachers of Mathematics, 1968.

Elisha Scott Loomis, Ph.D., LL.B., was professor of mathematics at Baldwin University for the period 1885-95 and head of the mathematics department at West High School, Cleveland, Ohio, for the period 1895-1923.
 
See also: Sketch of Pythagoras Curiosity.