Geometry Problem 1: Unlocking Geometric Mysteries: Discover the Hidden Angle in a Triangle with a 45-Degree Twist! Ideal for High School, College, and Math Enthusiasts-No Trigonometry, Just Pure Geometry!

Given a triangle ABC, let BD be the median such that angles A and DBC are equal. If angle ADB measures 45 degrees, find the measure of angle A. Please use elementary geometry, such as Euclid's Elements.

Uncover and share solutions to this problem.

Key Terms, Descriptions, and Solution Tips for the Geometric Problem

Key Term	Description and Solution Tips
Triangle ABC	A triangle with vertices labeled A, B, and C. Tip: Label all given angles and sides clearly. Look for relationships between angles, particularly those involving equal angles.
Median BD	A line segment from vertex B to point D, where D is the midpoint of side AC. Tip: Use the property that a median divides a triangle into two smaller triangles of equal area.
Angle A	The angle at vertex A in triangle ABC to be determined. Tip: Relate angle A with angle DBC. Remember that angle DBC is also equal to angle A.
Angle DBC	The angle formed between line segments BD and BC, equal to angle A. Tip: Since angle DBC equals angle A, explore triangle symmetry or congruence properties.
Angle ADB	The angle formed between line segments AD and BD, given as 45 degrees. Tip: Consider the properties of a 45-45-90 triangle and how this can help identify other angles in the problem.
45-45 Special Right Triangle	A right triangle where both of the non-right angles are 45 degrees, resulting in two equal sides. Tip: Look for right triangles formed by medians, bisectors, or auxiliary lines. Use their properties to deduce angle measures.
30-60 Special Right Triangle	A right triangle with angles of 30 and 60 degrees; side lengths are in the ratio 1:√3:2. Tip: While not directly given, consider constructing or identifying any 30-60-90 triangles in the solution process.
Isosceles Triangle	A triangle with two equal sides and two equal angles opposite those sides. Tip: Identify if triangle ABD or CBD could be isosceles, as this can simplify finding missing angles.
Equilateral Triangle	A triangle with all three sides and angles equal, each angle measuring 60 degrees. Tip: Although not directly involved, the properties of equilateral triangles might help if auxiliary lines lead to identifying any equilateral triangles.
Circumcircle	A circle passing through all three vertices of a triangle. Tip: Consider constructing a circumcircle if a cyclic quadrilateral is formed. This may help relate angles subtended by the same arc.
Cyclic Quadrilateral	A quadrilateral with all vertices on a circle. Tip: Check if adding auxiliary lines creates a cyclic quadrilateral; use opposite angles being supplementary.
Similarity	Figures with the same shape but different sizes; their corresponding angles are equal, and their sides are proportional. Tip: Look for triangles that are similar by AA (Angle-Angle) similarity. This can help find proportional sides and unknown angles.
Midpoint	The point that divides a line segment into two equal parts. Tip: Use the property that D is the midpoint of AC to infer that triangles ABD and CBD have equal bases.
Exterior Angle Theorem	The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles. Tip: Apply this theorem to triangle ABD or CBD to relate exterior angles to interior angles.
Sum of Angles Theorem	The sum of the interior angles of a triangle is always 180 degrees. Tip: Use this basic property to check consistency and correctness of angle calculations.
Auxiliary Lines	Additional lines drawn to assist in solving geometric problems. Tip: Draw auxiliary lines such as altitudes, medians, or angle bisectors to create helpful triangles or other geometric shapes.
Elementary Geometry	Basic geometric principles and methods, like those in Euclid's Elements, used without trigonometry. Tip: Stick to classical constructions and logical reasoning rather than advanced trigonometric functions.

---

Flyer of problem 1 using iPad Apps

---

Poster and Typography of problem 1

---

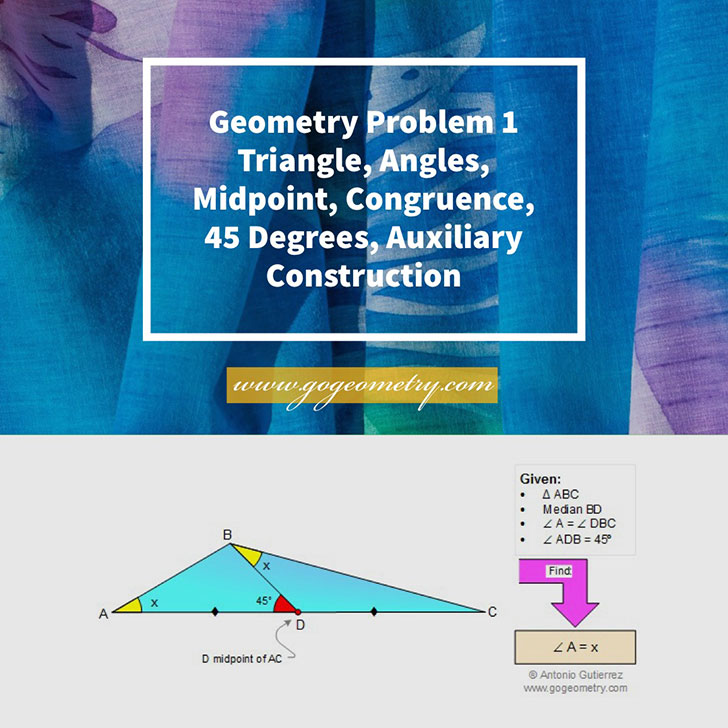
Geometric Art of problem 1

---

Mind Map: George Polya's 1945 book, "How to Solve It"