Online Geometry Problem 732: Triangle, Altitude, Orthic Triangle, Orthocenter, Congruence, Parallelogram. Level: High School, Honors Geometry, College, Mathematics Education

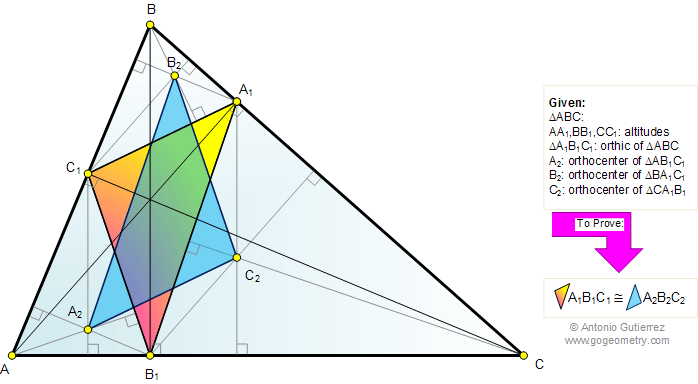
The figure shows a triangle ABC with the altitudes AA₁, BB₁, and CC₁. If A₂, B₂, and C₂ are the orthocenters of triangles AB₁C₁, BA₁C₁, and CA₁B₁, respectively, prove that the triangles A₁B₁C₁ and A₂B₂C₂ are congruent.
Note: The triangle A₁B₁C₁ is called the orthic triangle of the triangle ABC.