|
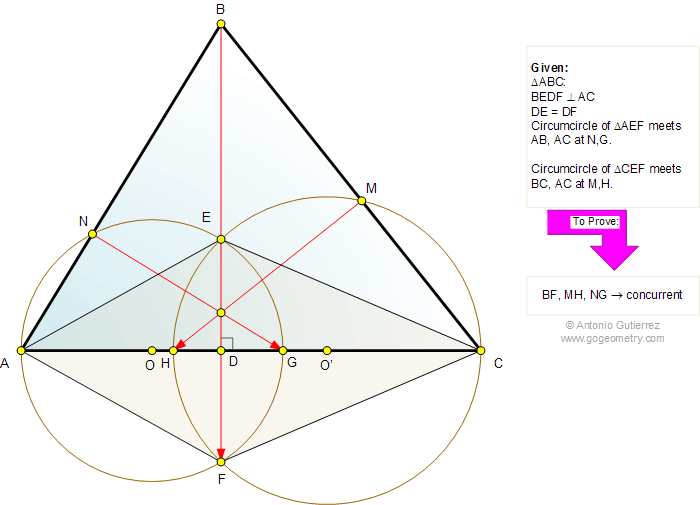
The diagram shows a triangle ABC with the
altitude BD. E is on BD and F is on BD extended such that DE = DF. The
circumcircle of triangle AEF meets AB and AC at N and G, respectively.
The circumcircle of triangle CEF meets BC and AC at M and H,
respectively. Prove that BF, MH, and NG are concurrent.
|