 |

|
Problem 548: Triangle, Transversal, Complete Quadrilateral,
Circumcircles, Circumcenters, Similarity, Concyclic
Points. Level: High School, SAT Prep, College
Geometry
|
|
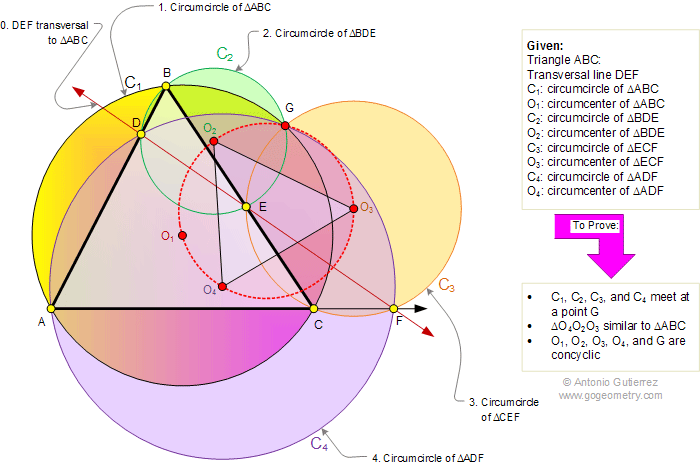
The figure shows a triangle ABC with a
transversal DEF (F on the extension of AC). O1, O2,
O3, and O4 are the circumcenters of triangles
ABC, BDE, ECF, and ADF, respectively. Prove that (1) the circumcircles
of triangles ABC, BDE, ECF, and ADF meet at a point G, (2) Triangles ABC
and O4O2O3. are similar, (3) O1,
O2, O3, O4, and G are concyclic points
(lie on a same circle).
Post a comment
or solution.
|
|
|
|
More Geometry Problems:
|
|
|
 |
Problem
547.
Triangle, Transversal, Four Circumcircles, Concurrency. |
|
|
 |
Typography and Sketch of Problem
548. |
|
|
 |
Problem
546.
Triangle, Angle Trisectors, 60 Degrees, Equilateral triangle. |
|
|
 |
Problem
545.
Acute Triangle, Squares, Altitudes, Area, Measure. |
|
|
|
|
|
 |
 |