Geometry Problems, Online Education

Problem 525: Circles, Diameter, Tangent, Radius, Congruence, Measurement. Level: High School, SAT Prep, College geometry

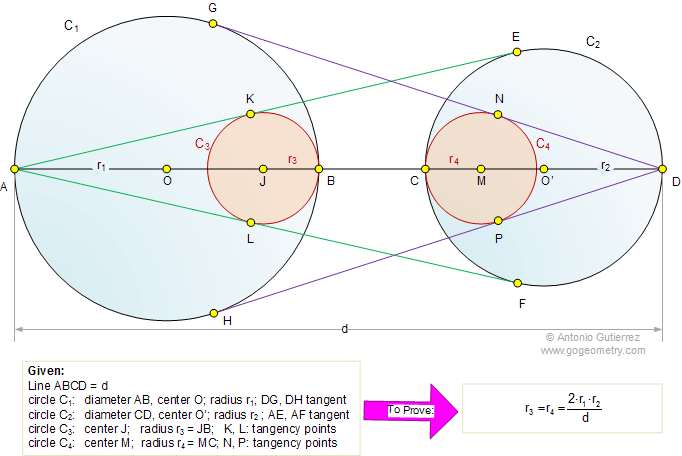
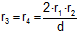The figure shows a line ABCD = d with circles C1 of diameter AB and circle C2 of diameter CD. AE and AF are tangent to circle C2, DG and DH are tangent to circle C1. Circle C3 of radius r3 is tangent to C1, AE and AF at B, K and L, respectively. Circle C4 of radius r4 is tangent to C2, DG and DH at C, N and P, respectively. Prove that Formula to prove.
 

Circles, tangent, inscribed circles, congruence, similarity
 

 

References:

Reference: Fukagawa Hidetoshi, Tony Rothman, "Sacred Mathematics: Japanese Temple Geometry" (Princenton University Press, 2008).
Between the seventeenth and nineteenth centuries Japan was totally isolated from the West by imperial decree. During that time, a unique brand of homegrown mathematics flourished, one that was completely uninfluenced by developments in Western mathematics. People from all walks of life—samurai, farmers, and merchants—inscribed a wide variety of geometry problems on wooden tablets called sangaku and hung them in Buddhist temples and Shinto shrines throughout Japan.

Equilateral triangle, Circumcircle

Problem 526.
Equilateral Triangle, Chord, Measurement.

Circle with equilateral triangles

Problem 524.
Circle, Equilateral Triangles, Midpoint, Side, Measurement.

Tangent Circles

Problem 523.
Tangent Circles, Diameter Perpendicular, Collinearity.

Geometry Problem: Right triangle, Circle, Tangent

Problem 522.
Right Triangle, Circle, Diameter, Tangent.

Triangle with six Squares

Triangle with Squares and Rectangles

Home | Search | Geometry | Problems | Art | All Problems | Sangaku | 521-530 | Diameters and Chords | Semicircle | Email | Post a comment or solution | By Antonio Gutierrez