|
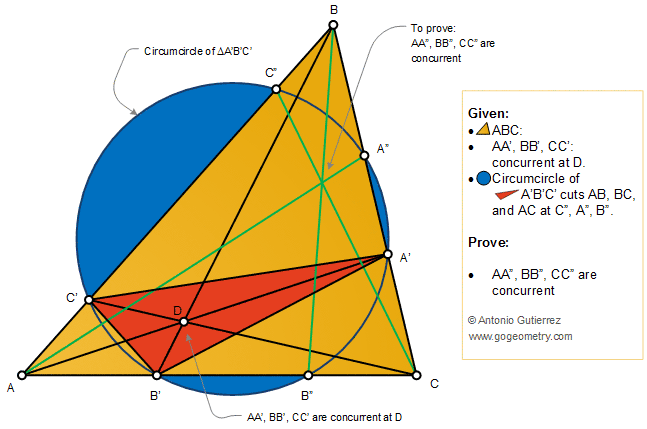
The figure shows a triangle ABC with
the concurrent cevians AA', BB', and CC'. The circumcircle of
triangle A'B'C' cuts AB, BC, and AC at C", A", and B",
respectively. Prove that the cevians AA", BB", and CC" are
concurrent.
Circumcircle of a triangle is the circle which
passes through the vertices. A cevian is a segment which joins a
vertex of a triangle with a point on the opposite side (or its
extension).
|