Geometry Problem 482: Co-Circularity of Incenter, Excenter, and Two Vertices in a Triangle Inscribed in Circumcircle

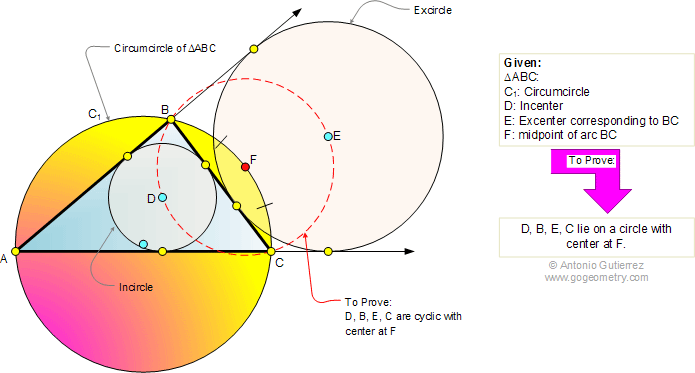
The figure shows a triangle ABC with circumcircle C₁, incenter D, and excenter E corresponding to BC. If F is the midpoint of arc BC, prove that points D, B, E, and C lie on a circle with the center at F.
The circumcircle of a triangle is the circle that passes through the vertices. The incenter is the center of the incircle, and the excenter is the center of an excircle.".