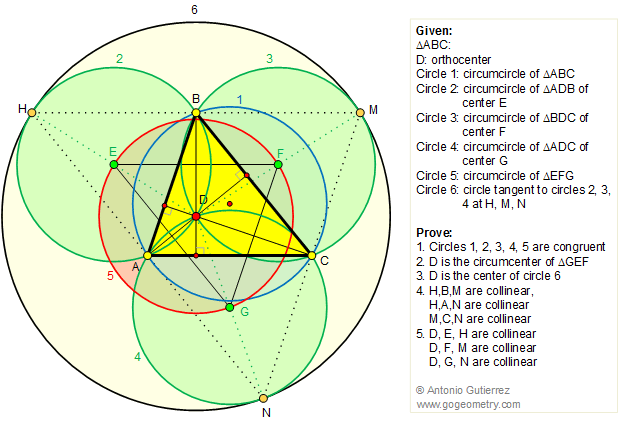
The figure shows a triangle ABC with the orthocenter D (point where altitudes intersect). Circles 1, 2 (center E), 3 (center F), 4 (center G), and 5 are the circumcircles of triangles ABC, ADB, BDC, ADC, and EFG, respectively. Circle 6 is tangent to circles 2, 3, and 4 at points H, M, and N, respectively. Prove that: (1) Circles 1,2,3,4,5 are congruent. (2) D is the center of circle 5. (3) D is the center of circle 6. (4) Points H,B,M are collinear, H,A,N are collinear, and M,C,N are collinear. (5) Points D,E,H are collinear, D,F,M are collinear, and D,G,N are collinear. .